Теорема Стюарта. Доказательство
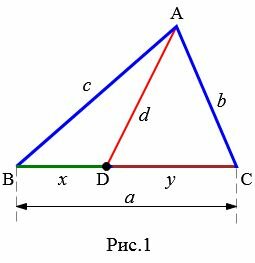
Теорема (Теорема Стюарта). Если точка D лежит на стороне BC треугольника ADC(Рис.1), то имеет место следующее равенство:
или
Доказательство (через теорему косинусов). Для треугольников ADB ADC запишем формулу, используя теорему косинусов:
Учитывая, что \( \small \cos ∠ADC=\cos (180°−∠ADB)=-cos∠ADB , \) (2) можно записать так:
Умножим (1) на y и (2') на x:
Сложим (3) и (4):
или
Тогда, учитывая, что x+y=a, получим:
Доказательство (с использованием векторов). Имеем:
Умножим (5) на CD, а (6) на BD:
Сложим (7) и (8):
Так как векторы 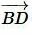 и
и 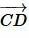 коллинеарны и имеют противоположные направнения, то
коллинеарны и имеют противоположные направнения, то
Учитывая (10) и CD+BD=BC, найдем AD из (9)
Возведем обе части равенства (11) в квадрат:
Далее
Возведем обе части равенства (12) в квадрат:
Поскольку
и, аналогично,
то
Тогда, учитывая (14),(15) и 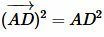 , упростим (12):
, упростим (12):
и , учитывая, что \( \small BD+CD=BC , \) получим:
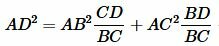
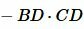
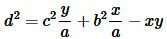 .
.
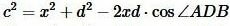 ,
,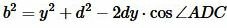 .
.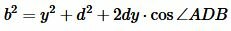 .
.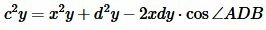 ,
,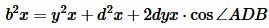 .
.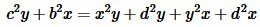 .
.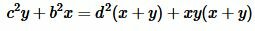 .
.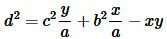 .
.
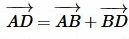 ,
, .
.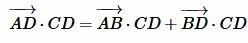 ,
,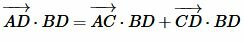 .
.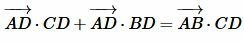
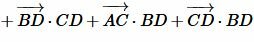 ,
,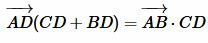
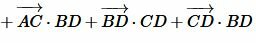 .
.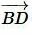 и
и 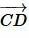 коллинеарны и имеют противоположные направнения, то
коллинеарны и имеют противоположные направнения, то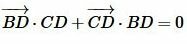 .
.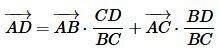 .
.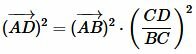

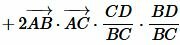 .
.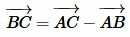 .
.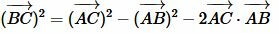 .
. .
.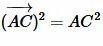 ,
,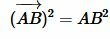 ,
,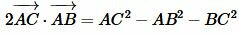 .
.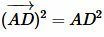 , упростим (12):
, упростим (12):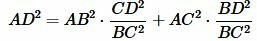
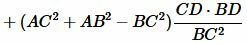
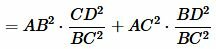
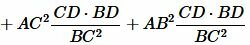
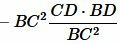
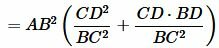
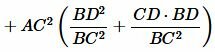
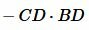 .
.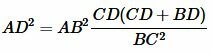
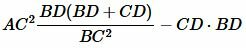
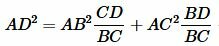
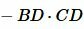 .
.