Теорема 1 (теорема синусов). Стороны треугольника пропорциональны синусам противолежащих углов:
 . |
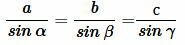(a) |
Доказательство. Пусть задан треугольник ABC. Проведем высоту hb из вершины B на сторону b (Рис.1).
 |
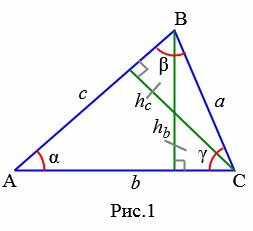Из определения синуса (см. страницу Синус и косинус. Онлайн калькулятор) следует, что синус угла α равен hb если предполагать, что c=1. Но поскольку c может иметь любое значение, то имеем
 |
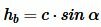Аналогично можем записать:
 |
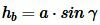Тогда имеем:
 |
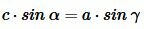или
 |
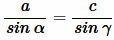(1) |
Далее, для высоты hc, опущенной из вершины C на сторону c, имеем:
 ,  . |
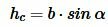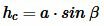Тогда
 |
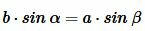или
 . |
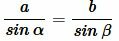(2) |
Из (1) и (2) получим:
| . |
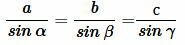Теорема доказана.
Теорема 2 (расширенная теорема синусов). Для произвольного треугольника справедливо следующее равенство:
 , |
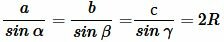(b) |
где a, b, c стороны треугольника, а α, β, γ противолежащие им углы, соответственно, R− радиус описанной около треугольника окружности.
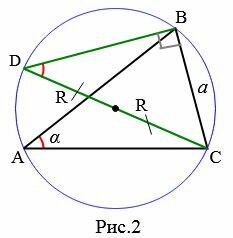
Доказательство. Пусть задан треугольник ABC и описанная окружность с радиусом R, проходящей через вершины треугольника.
 |
В теореме 1 мы доказали справедливость равенства (a). Для доказательства (b) достаточно показать, что
 . |
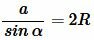(3) |
Проведем через вершину C диаметр CD описанной окружности и соединим точки D и B.
1. Пусть точки D и A лежат по одну сторону от BC (Рис.2). Полученный треугольник BCD являестся прямоугольным треугольником с прямым углом B, поскольку его одна сторона совпадает с диаметром окружности. А для этого прямоугольного треугольника справедливо равенство:
 . |
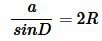Но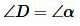 
поскольку обе эти углы опираются на дугу BC. Отсюда следует справедливость равенства (3).
2. Пусть точки D и A лежат в разные стороны от BC (Рис.3).
 . |
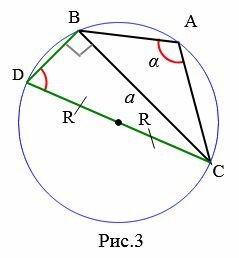Поскольку BCD прямоугольный треугольник, то справедливо следующее равенство:
| . |
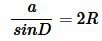(4) |
Покажем, что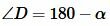 
. Действительно. Так как вписанный угол измеряется половиной дуги, на которой он упирается, то имеем:
 ,  . |
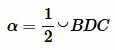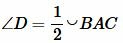(5) |
Очевидно, что
 . |
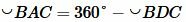(6) |
Тогда из (5) и (6) получим:
  . |
  . |
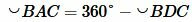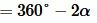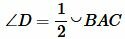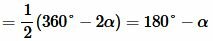(7) |
Учитывая (7), уравнение (4) можно записать так:
 . |
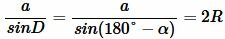(8) |
Но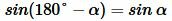 
. Тогда из (8) получим равенство (3).
Теорема доказана.
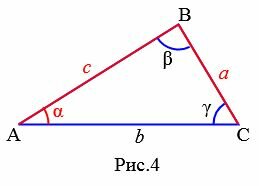
Задание 1. В треугольнике ABC a=8, c=10, угол α=30°. Найти сторону b (Рис.4).
 |
Решение. Из теоремы синусов, имеем:
 |
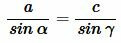Тогда
  |
 . |
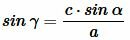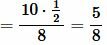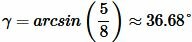Поскольку сумма всех углов треугольника равна 180°, то β=180°−30°−36.68°=113.32°.
Далее, из теоремы синусов:
 , |
  |
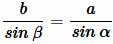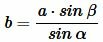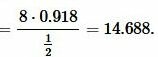Ответ: b=14.688.
Задание 2. В треугольнике ABC c=16, α=30°, β=45°. Найти стороны a, b (Рис.5).
 |
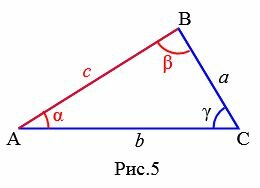Решение. Найдем сначала угол γ:
 , |
Из теоремы синусов имeем:
 , |
  . |
 , |
  . |
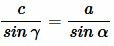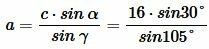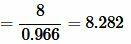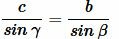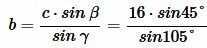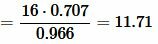Ответ: a=8.282, b=11.71.