С помощю этого онлайн калькулятора можно найти площадь треугольника. Для нахождения площади треугольника введите известные данные в ячейки и нажмите на кнопку "Вычислить". Теоретическую часть смотрите ниже.
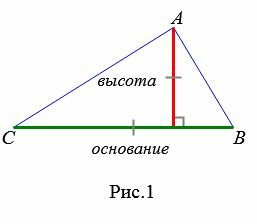
Любой из сторон треугольника можно называть основанием треугольника. Если основание выбрана, то под словом "высота" понимают высоту треугольника, проведенную к основанию (Рис.1):
 |
Теорема 1. Площадь треугольника равна половине произведения его основания на высоту.
Доказательство. Пусть AC основание треугольника ABC (Рис.2).
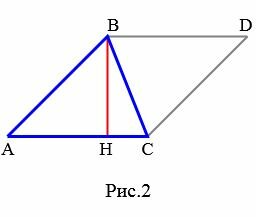 |
Проведем высоту BH. Обозначим через S площадь треугольника. Докажем, что
| \( \small S= \frac {\large 1}{\large 2} \cdot AC \cdot BH. \) |
Из вершины B проведем прямую, параллельную стороне AC, а из C − прямую, параллельную стороне AB. Поскольку \( \small AC \ || \ BD \) и \( \small AB\ || \ CD \), то ABDC является параллелограммой и, следовательно, \( \small AC \ = \ BD \), \( \small AB\ = \ CD . \) Тогда треугольники ABC и BCD равны по трем сторонам (см. статью на странице Треугольники. Признаки равенства треугольников). Так как площадь параллелограмма ABDC равна \( \small S_{ABDC}=AC \cdot BH, \) то площадь треугольника ABC (и BCD)равна половине площади параллелограмма:
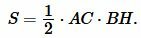  |
Следствие 1. Если высоты треугольников равны, то их площади относятся как основания.
Доказательство. Пусть площадь треугольников ABC и A1B1C1 равны:
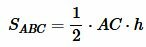 , , |
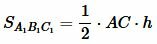 , , |
где AC и A1C1 основания треугольников ABC и A1B1C1, соответственно, а h их высоты.
Обозначим через k отношение
| \( \small k= \frac {\large AC}{\large A_1C_1}. \) |
Тогда
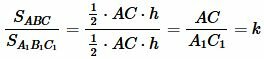 . . |
То есть отношение площадей треугольников с равными высотами равно отношению их оснований.
Следствие 2. Площадь прямоугольного треугольника равна половине произведения его катетов.
Действительно. Поскольку в прямоугольном треугольнике катеты перпендикулярны друг другу, то один из них можно определить как основание, а другой − как высоту. Тогда по теореме 1, площадь прямоугольного треугольника равна половине произведения его катетов.
Теорема 2. Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.
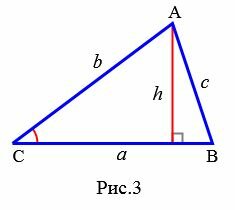
Доказательство. Обозначим через S площадь треугольника ABC и пусть a=BC, b=AC (Рис.3). Докажем, что
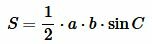 . . |
 |
Площадь данного треугольника можно вычислить по формуле, полученной выше (теорема 1):
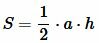 , , |
(1) |
где h − высота треугольника.
Из теоремы синусов имеем:
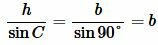 , , |
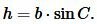 |
(2) |
Подставляя (2) в (1), получим:
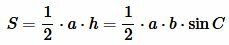 |
или
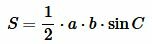  |
(3) |
Пусть известна сторона треугольника и две прилежащие углы (Рис.4).
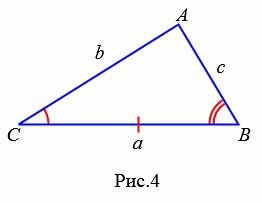 |
Найдем формулу площади этого треугольника. Обозначим через S площадь треугольника. Если у треугольника известны два угла, то можно найти и третий угол:
 |
(4) |
Найдем сторону b используя теорему синусов:
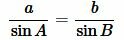 , , |
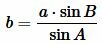 . . |
(5) |
В предыдующем параграфе мы вывели площадь треугольника по двум сторонам и углу между ними. Подставляя (4) и (5) в (3), получим:
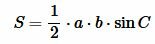 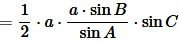 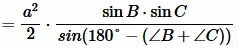 . . |
Учитывая формулы приведения тригонометрических функциий, получим:
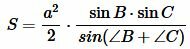 . . |
(6) |
Для нахождения площади треугольника по трем сторонам используют формулу Герона:
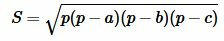 , , |
(7) |
где a, b, c − стороны треугольника, а p − полупериод треугольника:
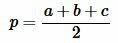 . . |
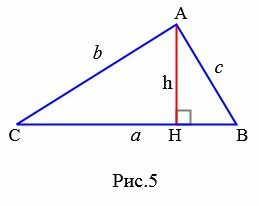 |
Доказательство формулы Герона. На рисунке 5 треугольник ABC имеет стороны a=BC, b=AC, c=AB. Проведем высоту h=AH. Обозначим x=CH. Тогда BH=a−x. Применим теорему Пифагора для треугольников AHC и AHB:
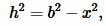 |
(8) |
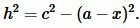 |
(9) |
Из (8) и (9) следует:
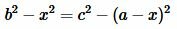 |
Откуда находим x:
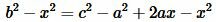 , , |
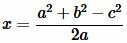 |
(10) |
Подставляя (10) в (8) найдем h:
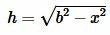 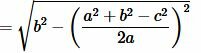 |
(11) |
Тогда площадь треугольника равна:
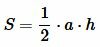 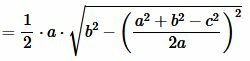 |
(12) |
Преобразовав (12) получим формулу (7):
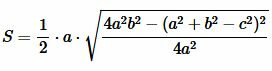 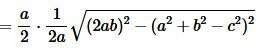 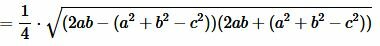 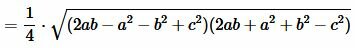 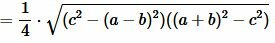 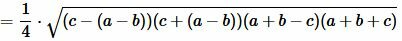 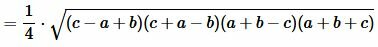 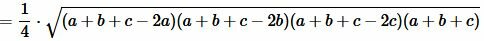 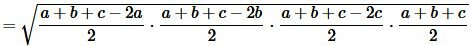 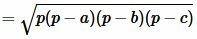 . . |
Пусть известны все три стороны треугольника и радиус описанной окружности (Рис.6). Докажем, что площадь треугольника равна: \( \small S=\frac{\large abc}{\large 4R}. \)
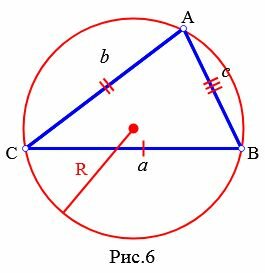 |
Из теоремы синусов имеем:
| \( \small \frac {\large a}{\large \sin A}= \frac {\large b}{\large \sin B} \) \(\small =\frac {\large c}{\large \sin C}=2R. \) |
Откуда;
| \( \small \sin C=\frac {\large c}{\large 2R}. \) | (13) |
Подставляя (13) в (3), получим:
| \( \small S=\frac {\large abc}{\large 4R}. \) | (14) |
Смотрите также: