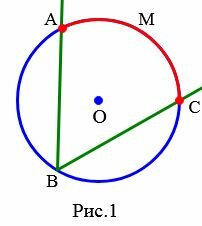
Определение 1. Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом окружности.
На рисунке 1 угол ABC вписанный. А дуга AMB расположена внутри этого угла. В таком случае говорят, что угол ABC опирается на дугу AMB.
 |
Теорема 1 (теорема о вписанном угле). Вписанный угол измеряется половиной дуги, на которую он опирается.
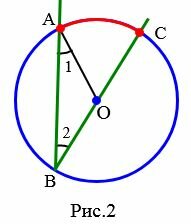
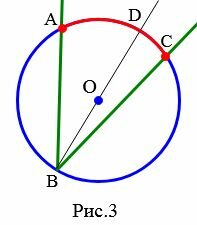
Доказательство. Пусть \( \small ABC \) -− вписанный угол окружности с центром O, которая опирается на дугу AC (Рис.2, Рис.3, Рис.4). Докажем, что 
   |
Возможны три случая расположения луча BO относительно угла ABC.
1. Луч BO совпадает с одним из сторон угла ABC, например со стороной BC (Рис.2). Поскольку в этом случае дуга AC меньше полуокружности, то  (см. статью Центральный угол окружности. Градусная мера дуги окружности).
(см. статью Центральный угол окружности. Градусная мера дуги окружности).
Рассмотрим треугольник ABO. Данный треугольник равнобедренный так как радиусы OA и OB окружности с центром O равны. Тогда \( \small \angle 1=\angle 2. \) Угол AOC является внешним углом треугольника ABO. Тогда \( \small \angle AOC=\angle 1+\angle 2 \) и поскольку \( \small \angle 1=\angle 2, \) получим: \( \small \angle AOC=2 \cdot \angle 2. \) Отсюда следует:
  |
или
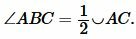 |
2. Луч BO делит угол ABC на два угла и не совпадает со стороной этого угла (Рис.3). Тогда луч BO пересекает дугу AC в некоторой точке D и делит ее на две дуги: AD и DC. По доказанному в пункте 1, имеем:
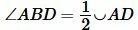 , , |
(1) |
 . . |
(2) |
Складывая равенства (1) и (2), получим:
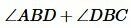 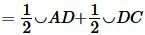 |
или
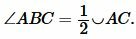 |
(3) |
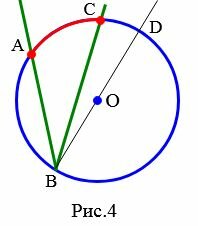
3. Луч BO не делит угол ABC на два угла и не совпадает со стороной этого угла (Рис.4). Тогда луч BO пересекает окружность с центром O в некоторой точке D. По доказанному в пункте 1, имеем:
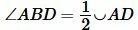 , , |
(4) |
 . . |
(5) |
Вычитая из (4) равенство (5), получим:
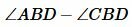 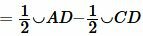 |
или
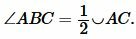  |
Следствие 1. Вписанные углы, опирающиеся на одну и ту же дугу, равны (Рис.5).
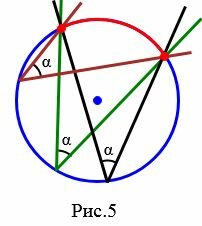 |
Следствие 2. Вписанный угол, опирающийся на полуокружность − прямой (Рис.6).
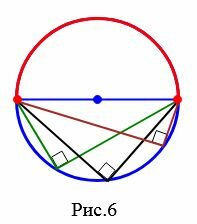 |
Теорема 2. Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
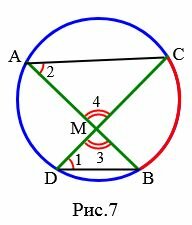 |
Доказательство. Пусть хорды AB и CD пересекаются в точке M. Докажем, что AM · MB=CM · MD (Рис.7). Углы 3 и 4 вертикальные, следовательно \( \small \angle 3=\angle 4 .\) Углы 1 и 2 равны, так как они опираются на одну и ту же дугу BC (Следствие 1). Следовательно треугольники AMC и DMB подобны по первому признаку подобия треугольников (см. Подобные треугольники. Признаки подобия треугольников). Тогда имеет место следующее соотношение \( \small \frac{AM}{MD}=\frac{CM}{MB}. \)
или
\( \small AM · MB=CM · MD. \) |