Перпендикулярные прямые

Рассмотрим две пересекающиеся прямые. Они образуют четыре неразвернутых угла.

Утверждение 1. Если один из углов пересекающих прямых − прямой, то остальные три угла также прямые.

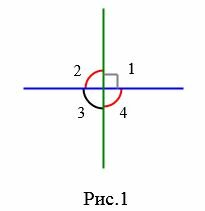Доказательство. Пусть угол 1 прямой (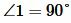)(Рис.1). Поскольку углы 1 и 2 смежные, то

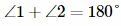Следовательно

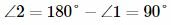Углы 2 и 4, а также 1 и 3 вертикальные. Тогда

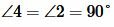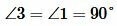Таким образом углы 1, 2, 3, 4 прямые.

Определение 1. Две пересекающиеся прямые называются перпендикулярными (взаимно перпендикулярными), если они образуют четыре прямых угла.

Если прямые AB и CD перпендикулярны, то это обозначается:

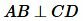и читается так: "прямая AB перпендикулярна прямой CD".

Теорема 1. Если две прямые перпендикулярны к третьей, то они не пересекаются.

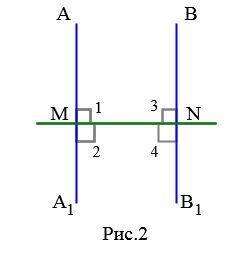Доказательство. Прямые AA₁ и BB₁ перпендикулярны к прямой MN (Рис.2). Тогда 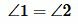(определение 1). Аналогично 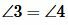. Перегнем мысленно рисунок по прямой MN так, чтобы верхняя часть рисунка наложилась на нижнюю. Из 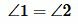и 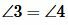следует, что луч MA наложится на луч MA₁, а луч NB − на NB₁.

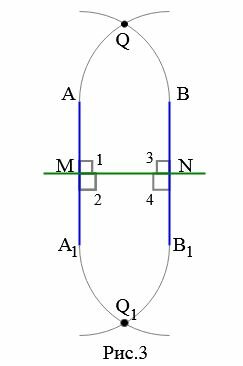Предположим, теперь, что прямые AA₁ и BB₁ пересекаются в некоторой точке Q (Рис.3). Тогда эта точка наложится на некоторую точку Q₁. Получается, что через две точки Q и Q₁ проходят две прямые AA₁ и BB₁. Но это невозможно. Следовательно предположение, что прямые AA₁ и BB₁ пересекаются неверно. То есть они не пересекаются.