С помощю этого онлайн калькулятора можно найти высоту треугольника. Для нахождения высоты треугольника введите известные элементы треугольника и нажмите на кнопку "Вычислить". Теоретическую часть смотрите ниже.
Определение 1. Отрезок, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.
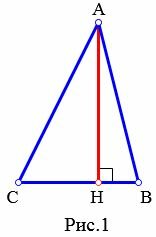 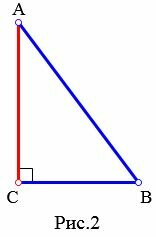 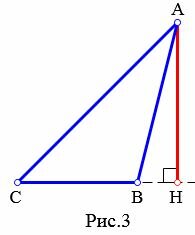 |
Высота треугольника может содержаться внутри треугольника (Рис.1), совпадать со стороной треугольника (при прямоугольном треугольнике высота совпадает с катетом (Рис.2) ), проходить вне треугольника (при тупоугольном треугольнике(Рис.3)).
Теорема 1. Все три высоты треугольника (или их продолжения) пересекаются в одной точке.
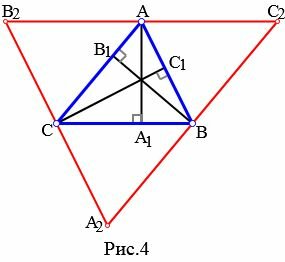 |
Доказательство. Рассмотрим произвольный треугольник ABC (Рис.4). Докажем, что высоты \( \small AA_1 ,\) \( \small BB_1 ,\) \( \small CC_1 \) пересекаются в одной точке. Из каждой вершины треугольника проведем прямую, параллельно противоположной стороне. Получим треугольник \( \small A_2B_2C_2. \) Покажем, что точки \( \small A, \ B, \ C \) являются серединами сторон треугольника \( \small A_2B_2C_2. \) \( \small AB=A_2C \) так как они являются противоположными сторонами параллелограмма \( \small ABA_2C. \) \( \small AB=CB_2 \) так как они являются противоположными сторонами параллелограмма \( \small ABCB_2. \) Тогда \( \small CB_2=CA_2, \) то есть точка \( \small C \) является серединой стороны \( \small A_2B_2 \) треугольника \( \small A_2B_2C_2. \) Аналогично доказывается, что точки \( \small A \) и \( \small B \) являются серединами сторон \( \small B_2C_2 \) и \( \small A_2C_2, \) соответственно.
Далее из \( \small AA_1⊥BC \) следует, что \( \small AA_1⊥B_2C_2 \) поскольку \( \small BC \ ǁ \ B_2C_2 \). Аналогично, \( \small BB_1⊥A_2C_2, \) \( \small CC_1⊥A_2B_2. \) Получили, что \( \small AA_1,\) \( \small BB_1, \) \( \small CC_1\) являются серединными перпендикулярами сторон \( \small B_2C_2, \) \( \small A_2C_2, \) \( \small A_2B_2, \) соответственно. Но серединные перпендикуляры треугольника пересекаются в одной точке (см. статью Серединные перпендикуляры к сторонам треугольника). Следовательно высоты треугольника или их продолжения пересекаются в одной точке.
Точка пересечения высот треугольника называется ортоцентром.
Пусть известны сторона треугольника и площадь. Найти высоту треугольника, отпущенная на известную сторону (Рис.5).
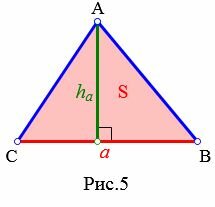 |
Решение. Площадь треугольника по основанию и высоте вычисляется из формулы:
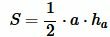 . . |
Откуда:
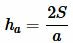 . . |
(1) |
Пример 1. Сторона треугольника равна \( \small a=5 \) а площадь \( \small S=7. \) Найти высоту треугольника.
Решение:
Применим формулу (1). Подставляя значения \( \small a \) и \( \small S \) в (1), получим:
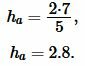 |
Ответ: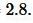
Формула площади треугольника по трем сторонам имеет следующий вид (см. статью на странице Площадь треугольника онлайн):
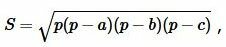 |
(2) |
где \( \small a, \ b, \ c \) стороны треугольника а полупериод \( \small p \) вычисляется из формулы:
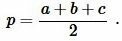 |
(3) |
Высота треугольника, отпущенная на сторону \( \small a\) вычисляется из формулы (1). Подставляя (2) в (1), получим формулу вычисления высоты треугольника по трем сторонам:
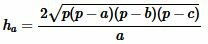 . . |
(4) |
Пример 2. Известны стороны треугольника: \( \small a=5, \) \( \small b= 4, \) \( \small c=7. \) Найти высоту треугольника, отпущенная на сторону \( \small a. \)
Решение: Найдем, сначала полупериод \( \small p \) треугольника из формулы (3):
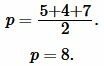 |
Подставляя значения \( \small a , \ b, \ c \) и \( \small p \) в (4), получим:
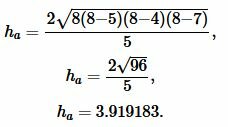 |
Ответ: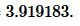
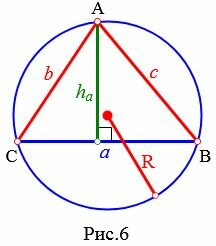 |
Рассмотрим треугольник на рисунке 6. Из теоремы синусов имеем:
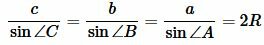 |
(5) |
откуда
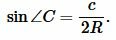 |
(6) |
Далее, из теоремы синусов имеем:
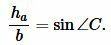 |
(7) |
Подставляя (6) в (7), получим:
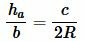 |
или
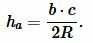 |
(8) |
Отметим, что радиус описанной окружности должен удовлетворять следующему неравенству:
| \(\small \max (b,c) ≤2R < b+c \) | (9) |
Пример 3. Известны стороны треугольника: \( \small b=7, \) \( \small c= 3 \) и радиус описанной окружности \( \small R=4. \) Найти высоту треугольника, отпущенная на сторону \( \small a. \)
Решение: Проверим сначала условие (9):
| \(\small \max (7,3) ≤2 \cdot 4 < 7+3 \) | (10) |
Условие (9) удовлетворяется, следовательно такой треугольник существует. Для нахождения выстоты треугольника воспользуется формулой (8). Имеем:
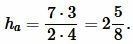 |
Ответ: \( \small 2\frac{5}{8}. \)
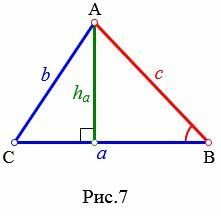 |
Найдем высоту \( \small h_a \) треугольника на рисунке 7. Из теоремы синусов имеем:
| \( \small \frac{\large h_a}{\large \sin \angle B}=\frac{\large c}{\large \sin 90°}, \) |
откуда
| \( \small h_a=c \cdot \sin \angle B. \) | (11) |
Пример 4. Известны сторона \( \small c=12 \) треугольника и прилежащий угол \( \small \angle B=30°. \) Найти высоту треугольника, отпущенная на сторону \( \small a. \)
Решение: Для нахождения высоты треугольника подставим значения \( \small c=12 \) и \( \small \angle B=30° \) в (11). Имеем:
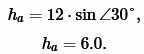 |
Ответ: \( \small 6. \)