С помощю этого онлайн калькулятора можно найти радиус вписанной в любой треугольник окружности, в том числе радиус вписанной в равносторонний треугольник окружности. Для нахождения радиуса вписанной в треугольник окружности выберите тип треугольника, введите известные данные в ячейки и нажмите на кнопку "Вычислить". Теоретическую часть и численные примеры смотрите ниже.
Пусть известна сторона a равностороннего треугольника (Рис.1). Выведем формулу вычисления радиуса вписанной в треугольник окружности.
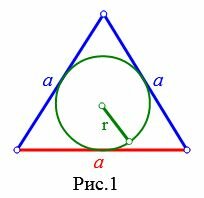 |
Радиус вписанной в равнобедренный треугольник окружности через основание a и боковую сторону b вычисляется из следующей формулы:
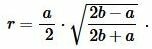 |
(1) |
Учитывая, что у равностороннего треугольника все стороны равны (\( \small a=b \)), имеем:
| \( \small r=\frac{\large a}{\large 2} \cdot \sqrt{\frac{\large 2a-a}{\large 2a+a}} \) \( \small =\frac{\large a}{\large 2} \cdot \sqrt{\frac{\large a}{\large 3a}} \) \( \small =\frac{\large a}{\large 2 \cdot \sqrt{3}} \) |
То есть
| \( \small r=\frac{\large a}{\large 2 \cdot \sqrt{3}} \) | (2) |
или, умножив числитель и знаменатель на \( \small \sqrt{3} \):
| \( \small r=\frac{\large \sqrt{3}}{\large 6 } \cdot a \) | (3) |
Пример 1. Известна сторона a=17 равностороннего треугольника. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся одним из формул (2) и (3). Подставим значения \( \small a=17 \) в (3):
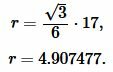 |
Ответ: 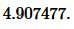
Пусть известна высота h равностороннего треугольника (Рис.2). Выведем формулу радиуса вписанной в треугольник окружности.
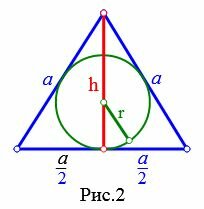 |
Выведем формулу стороны равностороннего треугольника через высоту. Из Теоремы Пифагора имеем:
| \( \small h^2+\left( \frac{\large a}{\large 2} \right) ^2=a^2.\) |
Тогда:
| \( \small h^2+ \frac{\large a^2}{\large 4} =a^2; \; \) \( \small \frac{\large 3}{\large 4}a^2 =h^2; \; \) \( \small a^2=\frac{\large4h^2}{\large 3}.\) |
Откуда:
| \( \small a= \frac{\large 2h}{\large \sqrt{3}} .\) | (4) |
Формула радиуса вписанной в равнобедренный треугольник окружности по основанию и высоте вычисляется из формулы
| \( \small r= \large \frac{a \cdot h}{a+\sqrt{a^2+4h^2}} \) | (5) |
Подставляя (4) в (5), получим:
| \( \small r= \large \frac{\frac{\large 2h^2}{\large \sqrt{3}}}{\frac{\large 2h}{\large \sqrt{3}}+\sqrt{\frac{\large 4h^2}{\large 3}+4h^2}} \) \( \small = \large \frac{\frac{\large 2h^2}{\large \sqrt{3}}}{\frac{\large 2h}{\large \sqrt{3}}+\sqrt{\frac{\large 16h^2}{\large 3}}} \) \( \small = \large \frac{\frac{\large 2h^2}{\large \sqrt{3}}}{\frac{\large 2h}{\large \sqrt{3}}+\frac{\large 4h}{\large \sqrt{3}}} \) \( \small = \large \frac{ 2h^2}{ 6h}\small =\large \frac{1}{3} \small \cdot h \) |
То есть, радиус вписанной в равносторонний треугольник окружности по высоте вычисляется из формулы:
| \( \small r = \large \frac{1}{3} \small \cdot h \) | (6) |
Пример 2. Известна высота \( \small h=39 \) равностороннего треугольника. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (6). Подставим значение \( \small h=39 \) в (6):
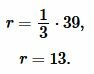 |
Ответ: 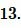
Пусть известна площадь S равностороннего треугольника (Рис.3). Найдем формулу радиуса вписанной в треугольник окружности.
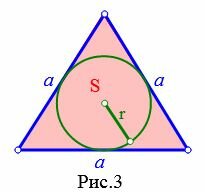 |
Площадь равностороннего треугольника по радиусу вписанной окружности вычисляется из следующей формулы:
| \( \small S= 3\cdot \sqrt{3}r^2.\) |
Откуда:
| \( \small r^2= \large \frac{S}{3 \cdot \sqrt{3}} \) \( \small = \large \frac{\sqrt{3} \ \cdot \ S }{9} \) |
Тогда:
| \( \small r= \large \frac{\sqrt[4]{3} }{3} \small \cdot \sqrt{S} \) | (7) |
Пример 3. Известна площадь равностороннего треугольника: \( \small S=42 . \) Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (7). Подставим значение \( \small S=42 \) в (7):
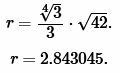 |
Ответ: 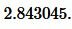
Смотрите также: