С помощю этого онлайн калькулятора можно найти площадь равностороннего треугольника. Для нахождения площади равностороннего треугольника введите известные данные в ячейки и нажмите на кнопку "Вычислить". Теоретическую часть и численные примеры смотрите ниже.
Пусть в равносторннем треугольнике известна сторона a (a=b=c) (Рис.1):
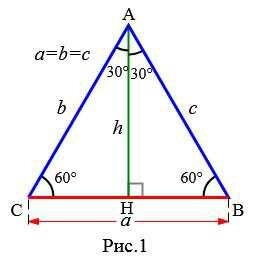 |
Найдем площадь треугольника. Поскольку в треугольнике напротив равных сторон расположенные равные углы (см. статью Соотношения между сторонами и углами треугольника), то в равносторннем треугольнике все углы равны. Но сумма всех углов треугольника равна 180°. Следовательно все три угла равностороннего треугольника равны 60°. Для треугольника ABH применим теорему синусов:
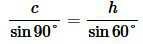 . . |
Учитывая, что 
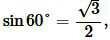
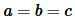 , получим:
, получим:
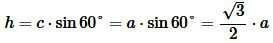 . . |
(1) |
Площадь треугольника по основанию и высоте имеет следующий вид:
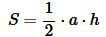 . . |
(2) |
Подставляя (1) в (2), получим:
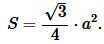 |
(3) |
Пример 1. Сторона равностороннего треугольника равна a=5. Найти площадь треугольника.
Решение. Для вычисления площади треугольника воспользуемся формулой (3). Подставляя значение a=5 в (3), получим:
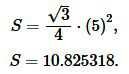 |
Ответ: 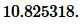
Пусть в равностороннем треугольнике известна высота h (Рис.1). Найдем площадь треугольника.
Найдем из формулы (1) a и подставим в (2):
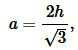 |
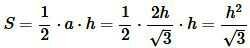 |
или
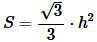 |
(4) |
Пример 2. Высота равностороннего треугольника равна h=6.5. Найти площадь треугольника.
Решение. Для вычисления площади треугольника воспользуемся формулой (4). Подставляя значение h=6.5 в (4), получим:
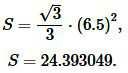 |
Ответ: 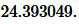
Пусть в прямоугольном треугольнике известна радиус вписанной окружности r (Рис.2):
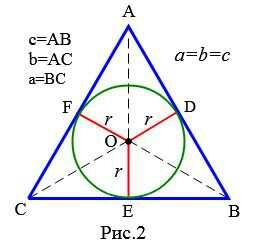 |
Найдем площадь равностороннего треугольника. На рисунке 2 равносторонний треугольник разделен га 6 частей. Полученные 6 прямоугольные треугольники равны по катету и гипотенузе (см. статью Прямоугольный треугольник). Тогда:
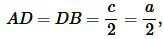 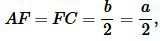 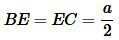 |
Чтобы найти площадь треугольника ABC достаточно найти площадь одного из прямоугольных треугольников и умножить на 6.
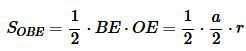 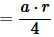 |
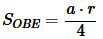 |
(5) |
Применим для треугольника OBE теорему синусов:
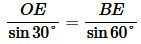 |
или
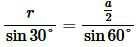 . . |
(6) |
Найдем a из формулы (6):
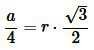 , , |
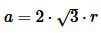 . . |
(7) |
Подставляя (7) в (5), получим:
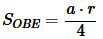 . . |
(8) |
Наконец, площадь треугольника ABC равна:
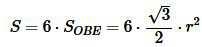 . . |
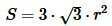 . . |
(9) |
Пример 3. Радиус вписанной окружности равностороннего треугольника равна r=7.5. Найти площадь треугольника.
Решение. Для вычисления площади треугольника воспользуемся формулой (9). Подставляя значение r=7.5 в (9), получим:
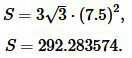 |
Ответ: 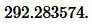
Пусть в прямоугольном треугольнике известна радиус описанной окружности R (Рис.3):
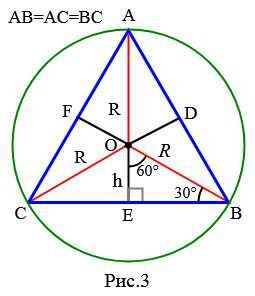 |
Найдем площадь равностороннего треугольника. На рисунке 3 равносторонний треугольник разделен на 6 частей. Полученные 6 прямоугольные треугольники равны по катету и гипотенузе. Тогда:
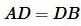 , , 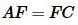 , , 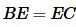 |
Чтобы найти площадь треугольника ABC достаточно найти площадь одного из прямоугольных треугольников и умножить на 6.
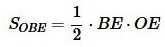 |
(10) |
Применим для треугольника OBE теорему синусов:
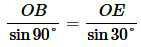 , , |
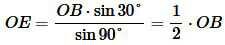 . . |
(11) |
Еще раз применим теорему синусов для треугольника OBE :
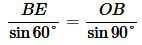 . . |
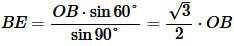 . . |
(12) |
Подставляя (11) и (12) в (10), получим:
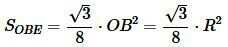 . . |
(13) |
Наконец, площадь треугольника ABC равна:
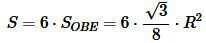 . . |
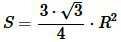 . . |
(14) |
Пример 4. Радиус oписанной окружности равностороннего треугольника равна R=11.2. Найти площадь треугольника.
Решение. Для вычисления площади треугольника воспользуемся формулой (14). Подставляя значение R=11.2 в (14), получим:
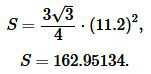 |
Ответ: 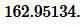
Смотрите также: