Определение 1. Серединным перпендикуляром к отрезку называется прямая, которая проходит через середину отрезка и перпендикулярная к нему.
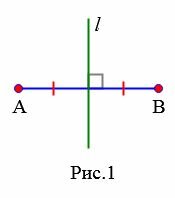 |
На рисунке 1 прямая \( \small l \) серединный перпендикуляр к отрезку \( \small AB .\)
Теорема 1. 1) Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. 2) Обратно: Каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.
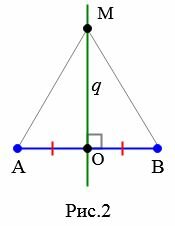 |
Доказательство. 1) Пусть точка \( \small O \) середина отрезка \( \small AB \) и пусть прямая \( \small q \) серединный перпендикуляр к отрезку \( \small AB \) (Рис.2). Рассмотрим любую точку \( \small M \) на прямой \( \small q \). Докажем, что \( \small AM=BM. \) Если точка \( \small M \) совпадает с точкой \( \small O \), то равенство \( \small AM=BM \) верно поскольку \( \small AO=BO \) (\( \small O \)-середина отрезка). Пусть \( \small M \) и \( \small O \) различные точки. Тогда прямоугольные треугольники \( \small MOA \) и \( \small MOB \) равны по двум катетам (\( \small AO=OB \), \( \small OM \)− общий). Следовательно \( \small AM=BM. \)
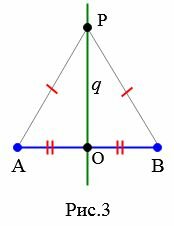 |
2) Пусть точка \( \small P \) равноудалена от от концов отрезка \( \small AB \) (Рис.3). Тогда выполено равенство \( \small AP=BP \). Докажем, что \( \small P \) лежит на серединном перпендикуляре \( q \). Если точка \( \small P \) принадлежит прямой \( \small AB \), то поскольку она равноудалена от концов отрезка \( \small AB, \) она совпадает с точкой \( \small O \), т.е. лежит на прямой \( q.\) Если же \( \small P \) не лежит на прямой \( \small AB \), то треугольник \( \small ABP \) равнобедренный, поскольку \( \small AP=BP .\) Отрезок \( \small PO \) медиана этого равнобедренного треугольника и, значит, является также высотой этого треугольника. Тогда \( \small PO⊥AB .\) Прямые \( \small PO \) и \( q \) проходят через точку \( \small O \) и перпендикулярны к \( \small AB .\) Следовательно эти прямые совпадают, т.е. точка \( \small P \) принадлежит прямой \( q. \)