Отрезки AB и CD пропорциональны отрезкам AB1 и CD1, если:
 |
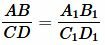(1) |
или
 |
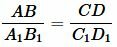(2) |
Отношением отрезков AB и CD называется отношение их длин, т.е. \( \frac {AB}{CD}. \)
Пример 1. На рисунке 1 заданы отрезки \( \small AB, \; CD, \; A_1B_1,\; C_1D_1. \) Определить, являются ли отрезки \( \small AB \) и \( \small CD \) пропорциональны отрезкам \( \small A_1B_1 \) и \( \small C_1D_1 \).
 |
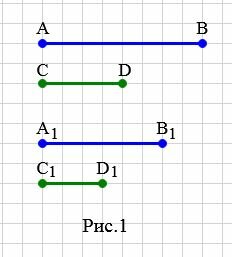Решение. Запишем длины отрезков:
  . |
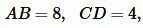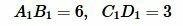Отношение отрезков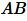 
и 
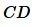равно:
 |
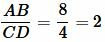Отношение отрезков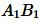 
и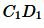 
равно:
 |
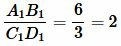Выполнено равенство
 , |
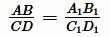значит отрезк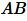и и 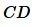пропорциональны отрезкам 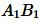и .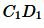
Легко убедится, что выполяется также равенство (2) (это следует также из правила перекрестного умножения):
 ,  . |
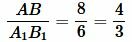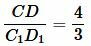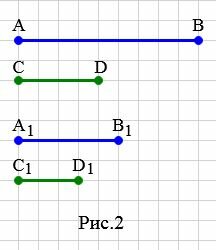
Пример 2. На рисунке 2 заданы отрезки \( \small AB, \; CD, \; A_1B_1,\; C_1D_1. \) Определить, являются ли отрезки \( \small AB \) и \( \small CD \) пропорциональны отрезкам \( \small A_1B_1 \) и \( \small C_1D_1 \).
 |
Решение. Запишем длины отрезков:
  . |
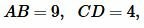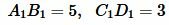Тогда
 ,  . |
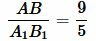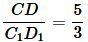Следовательно
 . |
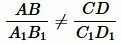Следовательно отрезк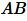и и 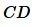не пропорциональны отрезкам 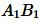и 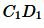.