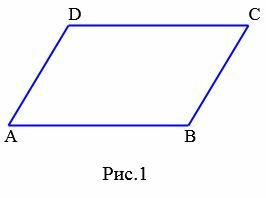
Определение 1. Параллелограммом называется четырехугольник, у которого противоположные стороны параллельны.
На Рис.1 изображен параллелограмм поскольку \( \small AB \ || \ CD, \;\; AD \ || \ BC .\)
 |
Свойство 1. В параллелограмме противоположные углы равны и противоположные стороны равны.
Доказательство. Рассмотрим параллелограмм ABCD (Рис.2).
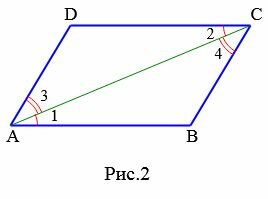 |
Диагональ AC разделяют параллелограмм на два треугольника ACB и ACD. \( \small \angle 1=\angle 2 \) поскольку эти углы накрест лежащие, при рассмотрении параллельных прямых AB и CD пересеченные секущей AC (см. теорему 1 статьи Теоремы об углах, образованных двумя параллельными прямыми и секущей). Аналогично \( \small \angle 3=\angle 4 \), если рассмотреть параллельные прямые AD и BC пересеченные секущей AC. Тогда треугольники ACB и ACD равны по одной стороне и двум прилежащим углам: AC общая, \( \small \angle 1=\angle 2 \), \( \small \angle 3=\angle 4 \) (см. статью Треугольники. Признаки равенства треугольников). Поэтому \( \small AB=CD, \;\; AD=BC, \;\; \angle B=\angle D. \)
Из рисунка Рис.2 имеем: \( \small \angle A=\angle 1+\angle 3, \;\; \angle C=\angle 2+\angle 4. \) Учитывая, что \( \small \angle 1=\angle 2 \) и \( \small \angle 3=\angle 4 \), получим: \( \small \angle A=\angle C. \)
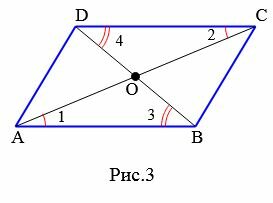
Свойство 2. Диагонали параллелограмма точкой пересечения разделяются пополам.
Доказательство. Рассмотрим параллелограмм ABCD (Рис.3) и пусть O точка пересечения диагоналей AC и BD. \( \small \angle 1=\angle 2 \) поскольку эти углы накрест лежащие, при рассмотрении параллельных прямых AB и CD пересеченные секущей AC. \( \small \angle 3=\angle 4 \), если рассмотреть параллельные прямые AB и CD пересеченные секущей BD. Поскольку в параллелограмме противоположные стороны равны: AB=CD (Свойство 1), то треугольники ABO и CDO равны по стороне и прилежашим двум углам. Тогда AO=OC и BO=OD.
 |
Признак 1. Если в четырехугольнике две стороны параллельны и равны, то этот четырехугольник является параллелограммом.
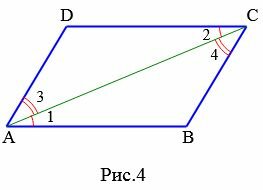 |
Доказательство. Рассмотрим параллелограмм ABCD. Пусть AB=CD и AB || CD. Проведем диагональ AC (Рис.4). Поскольку AB || CD, то \( \small \angle 1=\angle 2 \) как накрест лежащие углы − при рассмотрении параллельных прямых AB и CD пересеченных секущей AC. Тогда треугольники ACB и ACD равны, по двум сторонам и углу между ними. Действительно, AB=CD, AC− общая сторона \( \small \angle 1=\angle 2 \). Но тогда \( \small \angle 3=\angle 4. \) Рассмотрим прямые AD и BC, пересеченные секущей AC. Поскольку \( \small \angle 3 \) и \( \small \angle 4 \) являются накрест лежашими углами, то по теореме 1 статьи Параллельные прямые. Признаки параллельности прямых, эти прямые параллельны. Таким образом, в четырехугольнике противоположные стороны попарно параллельны (AB || CD, AD || BC) и, значит, данный четырехугольник параллелограмм.
Признак 2. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник является параллелограммом.
Доказательство. Рассмотрим параллелограмм ABCD (Рис.4). Проведем диагональ AC (Рис.4). Рассмотрим треугольники ACB и ACD. Эти треугольники равны по трем сторонам (см. статью Треугольники. Признаки равенства треугольников). Действительно. AC − общая для этих треугольников и по условию AB = CD, AD = BC. Тогда \( \small \angle 1=\angle 2 \). Отсюда следует AB || CD. Имеем, AB = CD, AB || CD и по признаку 1 четырехугольник ABCD является параллелограммом.
Признак 3. Если в четырехугольнике диагонали пересекаются и точкой пересечения разделяются пополам, то данный четырехугольник − параллелограмм.
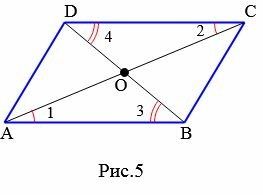 |
Доказательство. Рассмотрим четырехугольник ABCD (Рис.5). Пусть диагонали четырехугольника пересекаются в точке O и точкой пересечения делятся пополам:
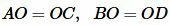 |
Углы AOB и COD вертикальные, следовательно \( \small \angle AOB=\angle COD \). Тогда треугольники AOB и COD равны по двум сторонам и углу меду ними:
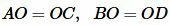 , , 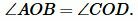 |
Тогда AB = CD и \( \small \angle 1=\angle 2 \). Но по признаку параллельности прямых следует, что AB || CD (теорема 1 статьи Параллельные прямые. Признаки параллельности прямых). Получили:
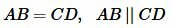 |
и, по признаку 1 четырехугольник ABCD − параллелограмм.