Ромб

Определение ромба

Определение 1. Ромб − это параллелограмм, у которого все стороны равны.

На рисунке 1 изображен ромб ABCD.

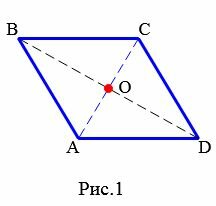Определение 2. Ромб − это четырехугольник, у которого все стороны равны.

Ромб разделяет плоскость на две части, одна из которых называется внутренней областью ромба, а другая внешней областью ромба.

Объединение ромба и ограниченной им части плоскости также называют ромбом.

Свойства ромба

Поскольку ромб является параллелограммом, то имеет следующие свойства:

• 1. У ромба противолежащие углы равны (\( \small \angle A = \angle C, \; \angle B = \angle D.\) )
• 2. У ромба противолежащие стороны равны (\( \small AB = DC, \; BC=AD.\) )
• 3. У ромба противолежащие стороны параллельны \( \small( AB \ || \ DC, \; BC \ || \ AD).\)
• 4. У ромба соседние углы дополняют друг друга до 180° \( \small ( \angle A +\angle B=180°, \) \( \small \angle C + \angle D=180°).\)
• 5. Диагонали ромба точкой пересечения делятся пополам \( \small ( AO = OC, \) \( \small BO=OD).\)

Ромб имеет также и следующие свойства:

• 6. Диагонали ромба пересекаются под прямым углом (\( \small AC \perp BD.\) )
• 7. Диагонали ромба являются биссектрисами его углов (\( \small \angle ABD = \angle CBD, \) \( \small \angle ADB = \angle CDB, \) \( \small \angle DAC = \angle BAC, \) \( \small \angle BCA = \angle DCA. \))
• 8. В любой ромб можно вписать окружность, центр которой лежит на пересечении его диагоналей.
• 9. Сумма квадратов диагоналей ромба равна квадрату стороны, умноженная на четыре \( \small (AC^2+BD^2=4AB^2). \)

Докажем свойства 6 и 7, сформулировав следующую теорему:

Теорема 1. Диагонали ромба перпендикулярны и являются биссектрисами его углов.

Доказательство. По определению 1, \( \small AD = DC \) (Рис.2). Следовательно треугольник \( \small DAC \) равнобедренный. Тогда \( \small \angle DCO = \angle DAO. \) Учитывая, что \( \small AO = OC \) (свойство 5 ромба), получим, что треугольники \( \small DOA \) и \( \small DOC \) равны по двум сторонам и углу между ними (см. статью Треугольники. Признаки равенства треугольников). Тогда равны углы DOC и DOA. Но эти углы смежные и их сумма равна 180°. Следовательно \( \small \angle DOC= \angle DOA=90°. \) То есть диагонали AC и BD перпендикулярны.

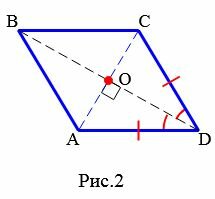Из равенства треугольников \( \small DOA \) и \( \small DOC \) также следует, что \( \small \angle CDO= \angle ADO,\) следовательно BD является биссектрисой угла ADС, то есть BD является биссектрисой ромба ABCD.

Признаки ромба

Признак 1. Если смежные стороны параллелограмма равны, то этот параллелограмм − ромб.

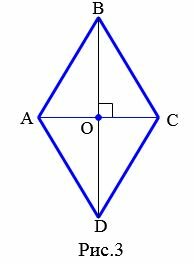Доказательство. Пусть смежные стороны параллелограмма ABCD равны. То есть имеем: AB=BC (Рис.3). У параллелограмма противоположные стороны равны (Свойство 1 статьи Параллелограмм). Тогда DC=AB=BC=AD. То есть все стороны параллелограмма равны и по определению 1, этот параллелограмм является ромбом.

Признак 2. Если диагонали параллелограмма перпендикулярны, то этот параллелограмм − ромб.

Доказательство. Пусть диагонали параллелограмма ABCD перпендикулярны (Рис.3). Рассмотрим прямоугольные треугольники AOB и COB. Так как у параллелограмма диагонали точкой пересечения разделяются пополам (Свойство 2 статьи Параллелограмм), то AO=OC. Тогда прямоугольные треугольники AOB и COB равны по двум катетам (AO=OC, BO общий катет (см. статью Прямоугольный треугольник. Свойства, признаки равенства)). Следовательно AB=BC. Тогда по признаку 1 этот параллелограмм является ромбом.

Признак 3. Если диагональ параллелограмма является биссектрисой его угла, то этот параллелограмм − ромб.

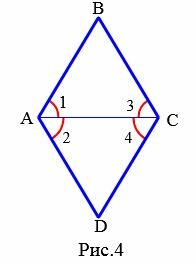Доказательство. Пусть диагональ AC параллелограмма ABCD является биссектрисой угла BAD (Рис.4). Тогда \( \small \angle 1= \angle 2 .\) У параллелограмма ABCD \( \small AB \ || \ DC .\) Тогда для параллельных прямых AB и DC и секущей AC справедливо равенство \( \small \angle 1= \angle 4 .\) (см теорему 1 статьи Теоремы об углах, образованных двумя параллельными прямыми и секущей). Аналогично, для параллельных прямых BC и AD и секущей AC справедливо равенство \( \small \angle 2= \angle 3 .\) Так как \( \small \angle 1= \angle 2 ,\) то \( \small \angle 1= \angle 2=\angle 3= \angle 4 .\) Из \( \small \angle 1= \angle 3\) следует, что треугольник ABC равнобедренный (Признак 2 статьи Равнобедренный треугольник). Тогда AB=BC. У параллелограмма противоположные стороны равны (Свойство 1 статьи Параллелограмм). Тогда AB=BC=CD=DA. То есть все стороны параллелограмма равны и по определению 1, этот параллелограмм является ромбом.

Признак 4. Если стороны четырехугольника равны, то этот четырехугольник − ромб.

Доказательство. Пусть у четырехугольника все стороны равны. Тогда этот четырехугольник является параллелограммом (признак 2 статьи Параллелограмм). А по определению 1, этот параллелограмм является ромбом.