С помощю этого онлайн калькулятора можно найти биссектрису треугольника. Для нахождения длины биссектрисы треугольника введите длины сторон треугольника, выберите сторону, к которой проведена биссектриса и нажмите на кнопку "Вычислить". Теоретическую часть смотрите ниже.
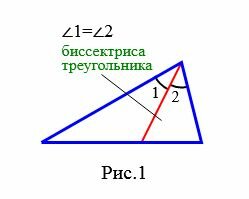
Определение 1. Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны называется биссектрисой треугольника (Рис.1).
 |
Биссектриса треугольника также называют биссектрисей угла треугольника или биссектрисей внутреннего угла треугольника.
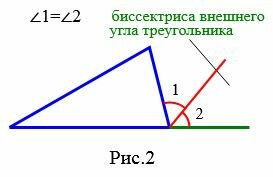
Биссектриса внешнего угла треугольника − это биссектриса угла, которая является смежным с внутренним углом треугольника (Рис.2).
 |
Любой треугольник имеет три биссектрисы.
Теорема 1. Биссектрисы треугольника пересекаются в одной точке.
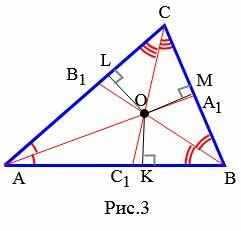 |
Доказательство. Проведем биссектрисы AA1, BB1 и обозначим через O точку их пересечения (Рис.3). Из точки O проведем перпендикуляры OK, OM и OL по сторонам треугольника ABC. По теореме 1 статьи Биссектриса угла. Свойства − OK=OL OK=OM. Следовательно OL=OM. Но последнее равенство означает, что точка O равноудалена от сторон AC и BC, т.е. находится на биссектрисе CC1 (Определение 2 статьи Биссектриса угла. Свойства).
Точка пересечения биссектрис треугольника называется инцентром треугольника. Инцентр треугольника является центром вписанной в треугольник окружности (Рис.4).
 |
Доказательство следует из теоремы 1, поскольку точка O равноудалена от сторон треугольника ABC и, следовательно, является центром окружности равной OK=OL=OM.
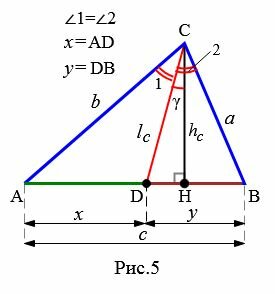
Рассмотрим треугольник на Рис.5.
 |
Длина биссектрисы треугольника можно вычислить следующими формулами:
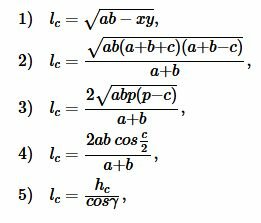 |
где p − полупериметр треугольника ABC, \( \small \gamma -\) угол между биссектрисой \( \small l_c\) и вершиной \( \small h_c:\)
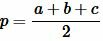 , , 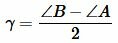 |
Доказательство. 1) Из теоремы Стюарта следует:
 |
(1) |
А из теоремы о биссектрисе треугольника следует, что если lc является биссектрисей треугольника ABC (Рис.5), то имеет место следующее соотношение:
 |
(2) |
Поскольку 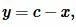 то (2) можно переписать так:
то (2) можно переписать так:
 |
(3) |
Найдем x из (3):
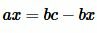 |
 |
(4) |
Тогда:
 |
или
 |
(5) |
Подставим (4) и (5) в (1):
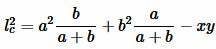  |
или
 . . |
(6) |
Cледовательно
 . . |
Доказательство. 2) Подставим (4) и (5) в (6):
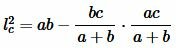 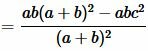 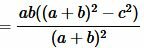 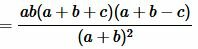 , , |
 . . |
(7) |
Тогда
 . . |
(8) |
Доказательство. 3) Сделаем следующее обозначение:
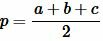 . . |
(9) |
Сделаем преобразования формулы (7), учитывая (9):
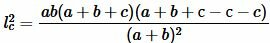 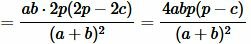 . . |
Следовательно
 . . |
(10) |
Доказательство. 4) Для доказательства четвертой формулы, снова обратимся к рисунке Рис.5. Запишем формулы площадей треугольников ABC, ADC и BDC:
 , , |
 , , |
 . . |
Учитывая, что 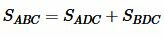 , получим:
, получим:
 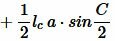 |
или
 . . |
Тогда
 . . |
(11) |
Для \( \small \sin C \) применим формулу синуса двойного угла:
 . . |
(12) |
Подставляя (12) в (11) получим:
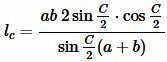 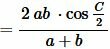 . . |
то есть
 . . |
(13) |
Доказательство. 5) Докажем пятую формулу. Из вершины C проведена вершина CH. Имеем прямоугольный треугольник CHD, для которого имеет место следующее равенство:
 . . |
Тогда
 . . |
Остается показать, что 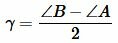 .
.
Поскольку биссектриса lc делит угол C пополам, то:
  . . |
(14) |
Далее
 . . |
Тогда
  . . |
(15) |
Подставляя (14) в (15), получим:
   |
или
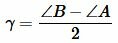 . . |