С помощю этого онлайн калькулятора можно найти радиус вписанной в треугольник окружности. Для нахождения радиуса вписанной в треугольник окружности введите известные данные в ячейки и нажмите на кнопку "Вычислить". Теоретическую часть и численные примеры смотрите ниже.
Пусть известна площадь S треугольника и полупериметр
| \( \small p=\frac{\large a+b+c}{\large 2 } \) | (1) |
где a, b, c стороны треугольника (Рис.1).
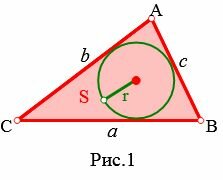 |
Найдем радиус вписанной в треугольник окружности r.
Из центра O вписанной в треугольник окружности проведем перпендикуляры к сторонам треугольника. Все эти перпендикуляры равны радиусу r вписанной в треугольник окружности (Рис.2).
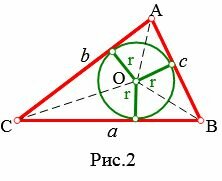 |
Прямыми OA, OB, OC разделим треугольник ABC на три треугольника: AOC, COB, AOB. Найдем площадь треугольников AOC, COB, AOB:
| \( \small S_{AOC}=\frac{\large 1}{\large 2} \cdot r \cdot b ,\) \( \small S_{AOB}=\frac{\large 1}{\large 2} \cdot r \cdot c, \) \( \small S_{BOC}=\frac{\large 1}{\large 2} \cdot r \cdot a \) | (2) |
Тогда имеем:
| \( \small S=S_{AOC}+S_{AOB}+S_{BOC}\)\( \small =\frac{\large 1}{\large 2} \cdot r \cdot b \) \( \small +\frac{\large 1}{\large 2} \cdot r \cdot c \) \( \small +\frac{\large 1}{\large 2} \cdot r \cdot a \) \( \small =\frac{\large 1}{\large 2} \cdot r \cdot ( a+b+c) \) | (3) |
или, учитывая (1):
| \( \small S=r \cdot p. \) | (4) |
Найдем радиус r вписанной в треугольник окружности из равенства (4):
| \( \small r=\frac{\large S}{\large p}. \) | (5) |
Пример 1. Известны площадь \( \small S=17 \) и полупериметр \( \small p=10 \) треугольника. Найти радиус вписанной в треугольник окружности.
Решение. Для нахождения радиуса вписанной в треугольник окружности воспользуемся формулой (5).
Подставим значения \( \small S=17 \) и \( \small p=10 \) в (5):
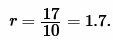 |
Ответ: 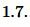
Пусть известны три стороны треугольника: a, b, c. Найдем радиус вписанной в треугольник окружности (Рис.3).
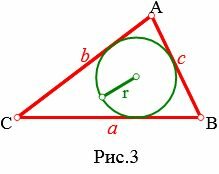 |
Площадь треугольника по трем сторонам вычисляется из формулы:
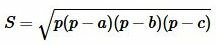 |
(6) |
где полупериметр p вычисляется из формулы (1).
Подставляя (6) в (5), получим формулу радиуса вписанной в треугольник окружности:
| \( \small r=\sqrt{\frac{\large (p-a)(p-b)(p-c)}{\large p}}, \) | (7) |
Пример 2. Известны стороны треугольника: \( \small a=15 ,\; b=7, \; c=9.\) Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанный в треугольник найдем сначала полупериметр треугольника из формулы (1):
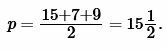 |
Подставим значения \( \small a,\; b, \; c, \; p \) в (7):
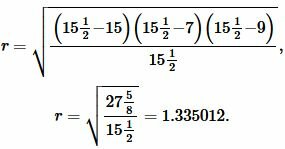 |
Ответ: 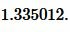
Пусть известны стороны b и c треугольника и угол A между ними (Рис.4). Найдем формулу радиуса вписанной в треугольник окружности.
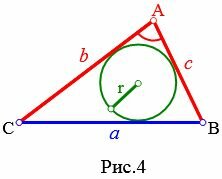 |
Из теоремы косинусов найдем сторону a треугольника:
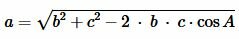 |
(8) |
Далее, для вычисления радиуса вписанной в треугольник окружности, воспользуемся формулой (7), где полупериметр p вычисляется из (1).
Пример 3. Известны стороны треугольника: \( \small b=9 ,\; c=7, \; \) и угол меджу ними A=30°. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанный в треугольник найдем сначала сторону a треугольника из формулы (8):
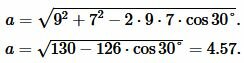 |
Далее найдем p из формулы (1):
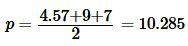 |
Подставим значения \( \small a,\; b, \; c, \; p \) в (7):
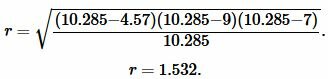 |
Ответ: 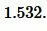
Пусть известны сторона a треугольника и прилежащие два угла B и C (Рис.5). Найдем радиус вписанной в треугольник окружности.
 |
Из теоремы синусов имеем:
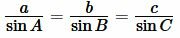 |
Тогда:
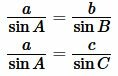 |
или
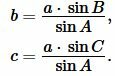 |
(9) |
Поскольку сумма углов треугольника равна 180°, то имеем \( \small \angle A=180°-(\angle B+\angle C). \) Из формул приведения тригонометрических функций имеем: \( \small \sin A=\sin (180°-( B+ C)) \) \( \small =\sin (B+C). \) Тогда формулы (9) можно переписать так:
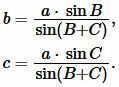 |
(10) |
Получая значения сторон b, c из (10) и значение p из (1), можно найди радиус вписанной в треугольник окружности из формулы (7). Таким образом, для нахождения радиуса вписанной в треугольник окружности через сторону и прилежащим двум углам применяется формула
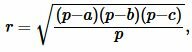 |
(11) |
где
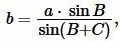 |
(12) |
 , , |
(13) |
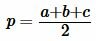 . . |
(14) |
Пример 4. Сторона треугольника равена: \( \small a=7 ,\) а прилежащие два угла равны соответственно \( \small \angle B=25°, \) \( \small \angle C=40°, \) Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (11). Найдем, сначала, стороны b и c из формул (12),(13). Подставим значения \( \small a=7 ,\) \( \small \angle B=25°, \) \( \small \angle C=40°, \) в (12) и (13):
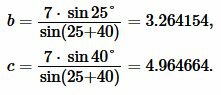 . . |
Далее найдем полупериметр p из формулы (14):
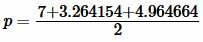 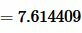 . . |
Подставляя значения a, b, c, p в (11), получим:
 |
Ответ: 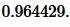
Смотрите также: