Теорема 1. Если две паралленльные прямые пересечены секущей, то накрест лежащие углы равны.
 |
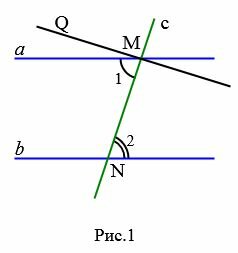Доказательство. Пусть параллельные прямые a и b пересечены секущей c (Рис. 1). Докажем,что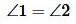 
. Предположим, что 
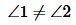. Отложим от луча MN угол QMN, равной углу 2 так, чтобы углы QMN и 2 были накрест лежащие при пересечении прямых QM и b секущей MN. Поскольку 
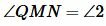, то 
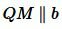. Получили, что через точку M проходят две прямые, параллельные прямой b, что противоречит аксиоме параллельных прямых (через точку не лежащую на данной прямой проходит только одна прямая, праллельная данной). Следовательно .
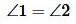Следствие 1. Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой.
 |
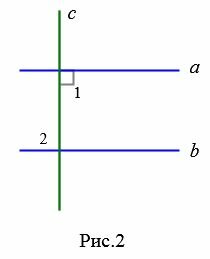Доказательство. Пусть прямые a и b параллельны (Рис. 2) и пусть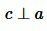 
(т.е.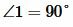 
). Прямая a пересекает прямую b (поскольку 
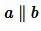). Но углы 1 и 2 накрест лежащие, следовательно они равы. Т.е. 
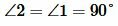. Следовательно прямые c и b перпендикулярны.
Теорема 2. Если две параллельные прямые пересечены секущей, то соответственные углы равны.
 |
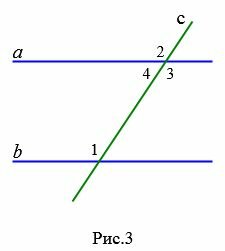Доказательство. Пусть параллельные прямые a и b пересечены секущей c (Рис.3). Тогда по теореме 1 накрест лежащие углы равны: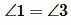 
. Углы 2 и 3 вертикальные, т.е. 
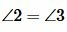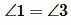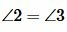. Из и имеем 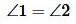. То есть при пересечении параллельных прямых секущей соответственные углы равны.
Теорема 3. Если две паралленльные прямые пересечены секущей, то сумма односторонних углов равна 180°.
Доказательство. Пусть параллельные прямые a и b пересечены секущей c (Рис.3). Покажем, что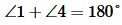 
. Накрест лежащие углы равны: 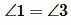. Углы 3 и 4 смежные. Поэтому 
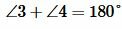. Тогда .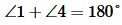