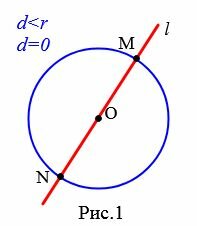
Выясним количество общих точек прямой и окружности в зависимости от их взаимного расположения. Если прямая l проходит через центр O окружности (Рис.1), то она пересекает окружность в двух точках, которые являются концами диаметра окружности.
Пусть прямая не проходит через центр окружности. Проведем перпендикуляр OH к прямой l (Рис.2, Рис.3, Рис.4). Обозначим расстояние от центра окружности до прямой l буквой d. Рассмотрим сколько общих точек будут иметь прямая и окружность в зависимости от соотношения d и r.
 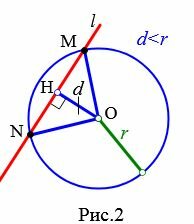 |
Теорема 1. Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность имеют две общие точки.
В этом случае прямая называется секущей по отношению к окружности.
Доказательство. Пусть расстояние от центра окружности до прямой меньше радиуса окружности: d<r (Рис.2). На прямой l от точки H отложим два отрезка HM и HN, которые имеют длину \( \small \sqrt{r^2-d^2}\) (Рис.2). Вычислим расстояния OM и ON используя теорему Пифагора:
| \( \small OM=\sqrt{OH^2+HM^2}\) \( \small \sqrt{d^2+(r^2-d^2)}=r\) |
| \( \small ON=\sqrt{OH^2+HN^2}\) \( \small \sqrt{d^2+(r^2-d^2)}=r\) |
Получили, что расстояние от центра окружности O до точек M и N равно r. Тогда эти точки лежат на окружности и являются общими для прямой l и данной окружности.
Докажем, далее, что прямая l и данная окружность не имеют других общих точек. Предположим, что они имеют еще одну общую точку P. Поскольку эта точка находится на окружности, то OM=OP=r. Тогда треугольник MOP равнобедренный и медиана OD, проведенная к основанию MP является высотой треугольника MOP. Поэтому \( \small OD ⊥ MP .\) Отрезки \( \small OD \) и \( \small OH \) не совпадают, так как середина D отрезка MP не совпадает с точкой H, которая является серединой отрезка MN. Получили, что из точки O проведены два перпендикуляра OH и OD к прямой l, что невозможно (см. статью Перпендикуляр к прямой). Таким образом, если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность имеют две общие точки.
Теорема 2. Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют одну общую точку.
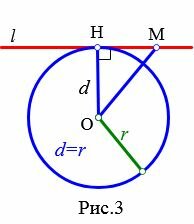 |
Доказательство. Пусть расстояние от центра окружности до прямой равно радиусу окружности: d=r (Рис.3). В этом случае OH=r, т.е. точка H лежит на окружности и является общей точкой прямой l и окружности. Возьмем на прямой l любую точку M отличной от H. Тогда расстояние от OM больше расстояния OH=r, поскольку наклонная OM больше перпендикуляра OH к прямой l. Следовательно точка M не лежит на окружности. Получили, что точка H единственная общая точка прямой l и окружности.
Теорема 3. Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общую точку.
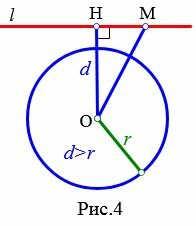 |
Доказательство. Пусть расстояние от центра окружности до прямой больше радиуса окружности:d>r (Рис.4). Тогда \( \small OH > r\). Возьмем на прямой l любую точку M отличной от H. Тогда \( \small OM > OH>r\). Следовательно точка M не лежит на окружности. Таким образом, если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общую точку.