С помощю этого онлайн калькулятора можно найти радиус описанной около треугольника окружности. Для нахождения радиуса окружности описанной около треугольника введите известные данные в ячейки и нажмите на кнопку "Вычислить". Теоретическую часть и численные примеры смотрите ниже.
Пусть известны три стороны a, b, c треугольника. Найдем радиус описанной окружности около треугольника.
Площадь треугольника по трем сторонам a, b, c и радиусу R описанной окружности имеет вид:
| \( \small S=\frac{\large abc}{\large 4R}, \) |
откуда
| \( \small R=\frac{\large abc}{\large 4S}. \) | (1) |
Площадь треугольника по трем сторонам имеет вид:
| \( \small S= \sqrt{p(p-a)(p-b)(p-c),}\) | (2) |
где
| \( \small p= \frac{\large a+b+c}{\large 2}. \) | (3) |
Подставляя (2) в (1), получим формулу радиуса описанной окружности около треугольника:
| \( \small R=\frac{\large abc}{\large 4\ \cdot \ \sqrt{p(p-a)(p-b)(p-c)}}. \) | (4) |
где p вычисляется из формулы (3).
Пример 1. Известны три стороны треугольника: \( \small a=6, \ b=5, \ c=4.5 \). Найти радиус окружности описанной около треугольника.
Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (4), где \( \small р \) вычисляется из формулы (3).
Найдем p из (2):
 |
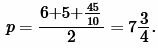Подставим значения a, b, c, p в (1):
 |
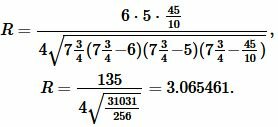Ответ: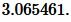 
Пусть известны сторона a и противолежащий угол A. Найдем радиус описанной окружности около треугольника. Из расширенной теоремы синусов имеем:
 . |
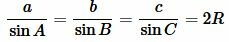Откуда:
 . |
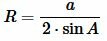(5) |
Пример 2. Сторона треугольника равна: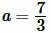 
а противолежащий угол \( \small \angle A=35°.\) Найти радиус окружности описанной около треугольника.
Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (5). Подставим значения 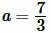и \( \small \angle A=35° \) в (5):
 . |
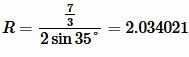Ответ: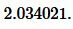 
Пусть известны стороны b и c треугольника и угол между ними A. Найдем радиус описанной окружности около треугольника.
Из теоремы косинусов, имеем:
 |
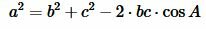или
 . |
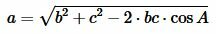(6) |
Подставляя (6) в (5), получим требуемую формулу:
 . |
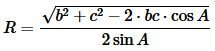(7) |
Пример 3. Известны две стороны треугольника: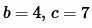 
и угол между ними: \( \small \angle A=30°. \) Найти радиус окружности описанной около треугольника.
Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (7). Подставим значения 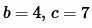и \( \small \angle A=30° \) в (7):
 . |
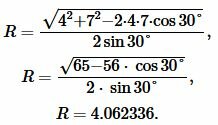Ответ: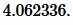 
Пусть известны сторона a треугольника и прилежащие к ней углы B и C. Найдем радиус описанной окружности около треугольника. Как известно, сумма углов треугольника равна 180°. Поэтому легко найти треий угол треугольника: \( \small \angle A=180°- (\angle B+ n\angle C). \) Тогда для нахождения радиуса описанной около треугольника окружности можно воспользоваться формулой (5):
   . |
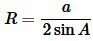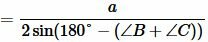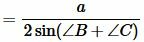Получили следующую формулу:
 . |
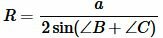(8) |
Пример 4. Известны сторона треугольника: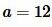 
и прилежащие к ней углы: \( \small \angle B=21°, \;\angle C=34°. \) Найти радиус окружности описанной около треугольника.
Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (8). Подставим значения 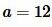и \( \small \angle B=21°, \;\angle C=34° \) в (8):
 |
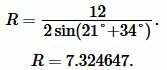Ответ: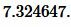 
Смотрите также: