С помощю этого онлайн калькулятора можно найти площадь прямоугольника. Для нахождения площади прямоугольника введите известные данные в ячейки и нажмите на кнопку "Вычислить". Теоретическую часть и численные примеры смотрите ниже.
Определение 1. Площадь прямоугольника − это величина той части плоскости, которую занимает прямоугольник.
Теорема 1. Площадь S прямоугольника со смежными сторонами a и b равна произведению этих сторон :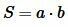
.
Доказательство. Рассмотрим прямоугольник со сторонами a, b и площадью S (Рис.1). Докажем, что .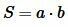
 |
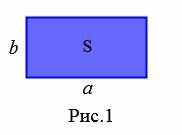Достроим прямоугольник до квадрата со стороной a+b (Рис.2). Площадь этого квадрата равна (a+b)·(a+b) (см. статью Площадь квадрата онлайн).
 |
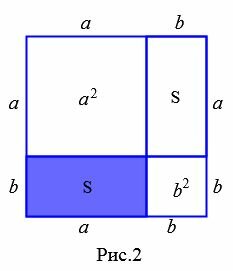С другой стороны, данный квадрат состоит из двух квадратов со сторонами со сторонами a и b и площадями a2 и b2, соответственно и из двух прямоугольников с площадями S. Поэтому сумма площадей этих двух квадратов и двух прямоугольников равна площади квадрата со стороной a+b:
 |
 . |
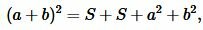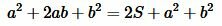Упрощая полученное равенство, получим: .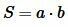
Из вышеизложенной теоремы следует, что площадь прямоугольника через его смежные стороны вычисляется из формулы:
|
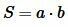(1) |
Пример 1. Стороны прямоугольника равны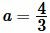 
и 
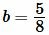. Найти площадь прямоугольника.
Решение. Для нахождения площади прямоугольника воспользуемся формулой (1). Подставим 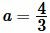, 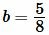в (1):
 |
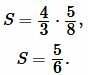Ответ: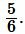 
Пример 2. Известна сторона прямоугольника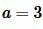 
и диагональ 
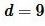(Рис.3). Найти площадь прямоугольника.
 |
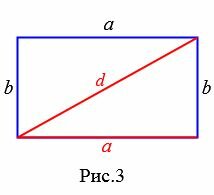Решение. Найдем сначала неизвестную сторону прямоугольника. Для этого воспользуемся теоремой Пифагора:
 |
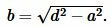(2) |
Площадь прямоугольника вычисляется из формулы (1). Подставляя (2) в (1), получим формулу вычисления площади прямоугольника через диагональ и сторону:
 |
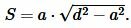(3) |
Подставим 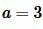, 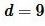в (3):
 |
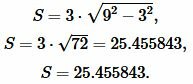Ответ: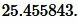 
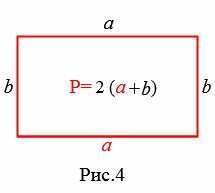
Пример 3. Известны сторона прямоугольника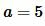 
и периметр 
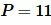(Рис.4). Найти площадь прямоугольника.
 |
Решение. Найдем сначала неизвестную сторону прямоугольника. Для этого воспользуемся теоремой Пифагора:
 |
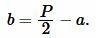(4) |
Площадь прямоугольника вычисляется из формулы (1). Подставляя (4) в (1), получим формулу вычисления площади прямоугольника через периметр и сторону:
 |
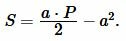(5) |
Подставим 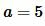, 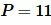в (5):
 |
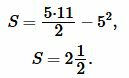Ответ: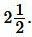 
Пример 4. Известны диагональ прямоугольника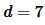 
и периметр 
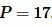(Рис.5). Найти площадь прямоугольника.
 |
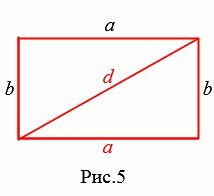Решение. Найдем сначала стороны прямоугольника. Запишем формулу Пифагора и формулу периметра прямоугольника:
 |
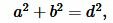(6) |
 |
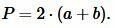(7) |
Из формулы (7) найдем \( \small b \) и подставим в (6):
 |
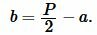(8) |
 |
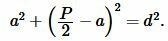(9) |
Упростив (9), получим квадратное уравнение относительно неизвестной \( a \):
 |
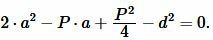(10) |
Вычислим дискриминант квадратного уравнения (10):
 |
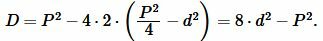(11) |
Подставляя значения 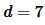и 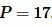в (11), получим:
 |
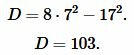Поскольку дискриминант неотрицательное число, то такой прямоугольник существует.
Стороны прямоугольника вычисляются из формул:
 |
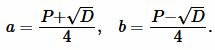(12) |
Почему \( \small b \), как и \( \small a \) получается неотрицательным, посмотрите "примечание" на странице Прямоугольник. Онлайн калькулятор.
Площадь прямоугольника по двум сторонам равна:
| \( \small S=a \cdot b \) | (13) |
Подставляя (12) в (13), получим:
| \( \small S=\frac{\large P^2-D}{\large 16} \) | (14) |
Далее, из (11) и (14) следует:
| \( \small S=\frac{\large P^2-4d^2}{\large 8}. \) | (15) |
Подставляя 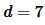, 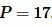в (15), получим:
 |
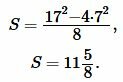Ответ: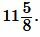 
Смотрите также: