С помощю этого онлайн калькулятора можно найти радиус описанной окружности около любого треугольника, в том числе радиус окружности около равностороннего треугольника. Для нахождения радиуса окружности описанной около треугольника введите известные данные в ячейки и нажмите на кнопку "Вычислить". Теоретическую часть и численные примеры смотрите ниже.
Пусть известна сторона a равностороннего треугольника. Найдем радиус описанной окружности около треугольника. На странице Радиус окружности описанной около треугольника вычисляется из формулы:
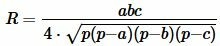 |
(1) |
где p вычисляется из формулы:
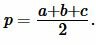 |
(2) |
Учитывая, что у нас треугольник равносторонний, т.е. a=b=c, имеем:
| \( \small p= \frac{\large 3a}{\large 2}, \) | (3) |
| \( \small p-a=p-b=p-c= \frac{ \large a}{ \large 2}. \) | (4) |
Подставляя (3),(4) в (1) и учитывая, что a=b=c, получим:
| \( \small R=\frac{\large a^3}{\large 4\ \cdot \sqrt{\frac{3}{2}a \left( \frac{a}{2} \right)^3}} \) \( \small =\frac{\large a^3}{\large 4 \ \cdot \ \sqrt{ \frac{3a^4}{16}}} \) \( \small =\frac{\large a}{ \large \sqrt{ 3}} \) |
то есть
| \( \small R=\frac{\large a}{ \large \sqrt{ 3}}=\frac{\large a \sqrt{3}}{ \large 3}. \) | (5) |
Пример 1. Известна сторона \( \small a=\frac{7}{2} \) равностороннего треугольника. Найти радиус окружности описанной около треугольника.
Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (5).
Подставим значение \( \small a=\frac{7}{2} \) в (5):
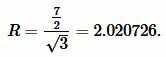 |
Ответ: 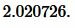
Пусть известна высота h равностороннего треугольник (Рис.1):
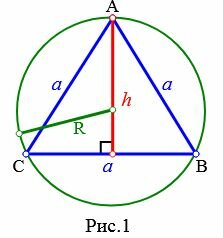 |
Найдем радиус описанной окружности около равностороннего треугольника. Из теоремы синусов имеем:
| \( \small \frac{\large a}{ \large \sin 90°}=\frac{\large h }{ \large \sin C}. \) | (6) |
Уситывая, что сумма углов треугольника равна 180° и что у равностороннего треугольника все углы равны, имеем: \( \small \angle A= \angle B=\angle C=60°. \) Тогда из (6) получим:
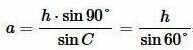 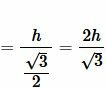 |
то есть
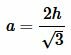 |
(7) |
Подставляя (7) в (5), получим:
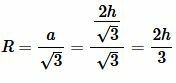 |
или
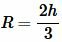 |
(8) |
Пример 2. Высота равностороннего треугольника равна:\( \small h=15 .\) Найти радиус окружности описанной около равностороннего треугольника.
Решение. Для нахождения радиуса окружности описанной около равностороннего треугольника воспользуемся формулой (8). Подставим значения \( \small h=15 \) в (8):
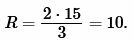 |
Ответ: 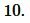
Пусть известна площадьS равностороннего треугольника. Найдем радиус окружности, описанной около треугольника. На странице Площадь равностороннего треугольника онлайн была выведена формула площади равностороннего треугольника по радиусу описанной окружности:
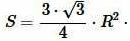 |
(9) |
В формуле (9) найдем R:
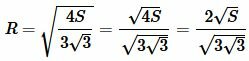 |
или
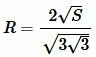 |
(10) |
Пример 3. Площадь равностороннего треугольника равна:\( \small S=14.5 .\) Найти радиус окружности описанной около равностороннего треугольника.
Решение. Для нахождения радиуса окружности описанной около равностороннего треугольника воспользуемся формулой (10). Подставим значения \( \small S=14.5 \) в (10):
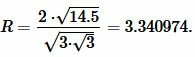 |
Ответ: 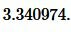
Смотрите также: