Теорема 1. Биссектриса при вершине треугольника делит противоположную сторону на две отрезки, пропорциональные сторонам, прилежащим к данной вершине. То есть если биссектриса при вершине A делит в точке D сторону BC на отрезки BD и CD (Рис.1), то имеет место следующее соотношение:
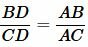 |
(1) |
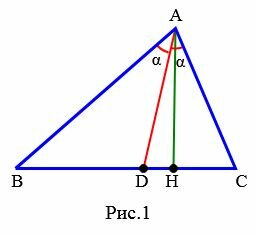 |
Доказательство (метод площадей 1). Из вершины A опущена биссектриса AD. Построим вершину треугольника AH. Найдем площади треугольников ABD и ACD:
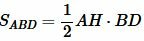 , , |
(3) |
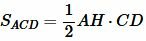 . . |
(4) |
Построим следующее соотношение
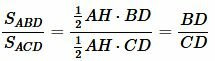 . . |
(5) |
С другой стороны, площадь треугольников ABD и ACD можно найти используя следующие формулы:
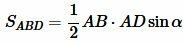 . . |
(6) |
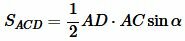 . . |
(7) |
Построим следующее соотношение используя формулы (6) и (7):
 . . |
(8) |
Из формул (5) и (8) получим соотношение (1).
Доказательство (метод площадей 2). С одной стороны, аналогично вышеизложенному имеем соотношение (5). Далее из точки D проведем вершины L и M для треугольников ABD и ACD (Рис.2).
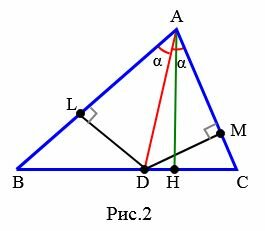 |
Тогда площади треугольников ABD и ACD можно найти из формул:
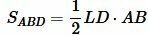 , , |
(9) |
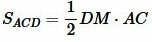 . . |
(10) |
Построим следующее соотношение
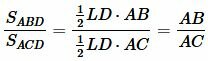 . . |
(11) |
Из формул (5) и (11) получим соотношение (1).
Доказательство (через теорему синусов). Рассмотрим треугольник ABC. Из точки A проведем биссектрису AD (Рис.3):
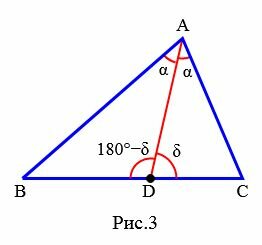 |
Применяя теорему синусов для треугольников ABD и ACD можем записать:
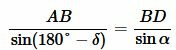 , , |
(12) |
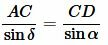 . . |
(13) |
Поделив (12) на (13) и учитывая, что \( \small \sin(180°-\delta)=\sin \delta , \) (см. статью Формулы приведения тригонометрических функций онлайн) получим равенство (1).
Доказательство (через подобие треугольников). Рассмотрим треугольник ABC. Из точки A проведем биссектрису AD (Рис.4). Проведем перпендикуляры из вершин B и C на луч AD и обозначим точки пересечения через L и K.
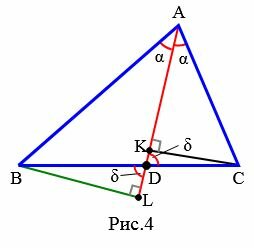 |
Рассмотрим треугольники ABL и ACK. Эти треугольники подобны по двум углам (\( \small ∠ ALB= ∠ AKC ,\;\; ∠ BAL= ∠ CAK \) ). Тогда имеем:
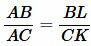 |
(14) |
Рассмотрим, далее, треугольники BLD и CKD. Они также подобны поскольку \( \small ∠ BLD= ∠ CKD ,\) а углы BDL и CDK равны так как они вертикальные. Тогда имеет место следующее соотношение:
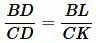 |
(15) |
Из равенств (14) и (15) получаем:
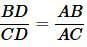 . . |
Пример. Даны стороны треугольника ABC: AB=18, AC=6, BC=20. Найти отрезки, полученные делением биссектрисей большой стороны треугольника.
Решение. Поскольку напротив самой большой стороны треугольника находится вершина A, то бисскетриса AD делит сторону BC на отрезки BD и CD. Тогда имеем:
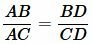 . . |
(16) |
Обозначим BD=x. Тогда CD=BC−x=20−x. Подставляя данные в уравнение (16), получим:
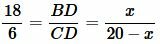 |
или
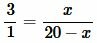 . . |
(17) |
Методом перекресного умножения упростим (17) и решим:
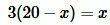 ; ; 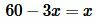 ; ; 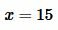 . . |
(18) |
Тогда BD=x=15, CD=BC−x=20−x=5.
Ответ. BD=15, CD=5.