С помощю этого онлайн калькулятора можно найти радиус вписанной в треугольник окружности, в том числе радиус вписанной в равнобедренный треугольник окружности. Для нахождения радиуса вписанной в треугольник окружности выберите тип треугольника, введите известные данные в ячейки и нажмите на кнопку "Вычислить". Теоретическую часть и численные примеры смотрите ниже.
Пусть известны известны основание a и боковая сторона b равнобедренного треугольника (Рис.1). Выведем формулу вычисления радиуса вписанной окружности через основание и боковую сторону.
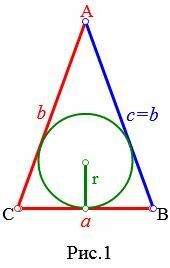 |
Радиус вписанной в треугольник окружности через три стороны a, b, c вычисляется из следующей формулы:
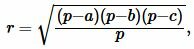 |
(1) |
где полупериметр p вычисляется из формулы:
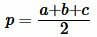 . . |
(2) |
Учитывая, что у равнобедренного треугольника боковые стороны равны (\( \small b=c \)), имеем:
| \( \small p=\frac{\large a+b+c}{\large 2} \) \( \small =\frac{\large 2b+a}{\large 2}, \) | (3) |
| \( \small p-a=\frac{\large 2b+a}{\large 2}-a \) \( \small =\frac{\large 2b-a}{\large 2}, \) | (4) |
| \( \small p-b=p-c=\frac{\large 2b+a}{\large 2}-b \) \( \small =\frac{\large a}{\large 2}. \) | (5) |
Подставляя (3)-(5) в (1), получим формулу вычисления радиуса вписанной в равнобедренный треугольник окружности:
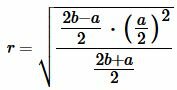 , , |
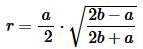 . . |
(6) |
Пример 1. Известны основание a=13 и боковая сторона b=7 равнобедренного треугольника. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (6). Подставим значения \( \small a,\; b \) в (6):
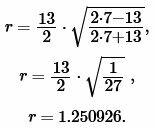 |
Ответ: 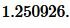
Пусть известны основание a и прилежащий к ней угол β равнобедренного треугольника (Рис.2). Выведем формулу радиуса вписанной в треугольник окружности.
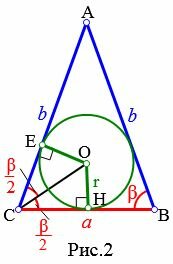 |
Из центра вписанной окружности проведем перпендикуляры OH и OE к сторонам a=BC и b=AC, соответственно (r=OH=OE). Соединим точки C и O. Полученные прямоугольные треугольники OCE и OCH равны по гипотенузе и катету (см. статью Прямоугольный треугольник. Тогда \( \small \angle OCE=\angle OCH=\frac{\large \beta}{\large 2}. \) Для прямоугольного треугольника OCH можно записать:
| \( \small \frac{\large OH}{\large HC}=\frac{\large r}{\large \frac{a}{2}}=\mathrm{tg}\frac{\large \beta}{\large 2} .\) |
Откуда получим формулу радиуса вписанной в треугольник окружности:
| \( \small r=\frac{\large a}{\large 2} \cdot \mathrm{tg}\frac{\large \beta}{\large 2} .\) | (8) |
Учитывая формулы половинного угла тригонометрических функций, формулу (8) можно записать так:
| \( \small r=\frac{\large a}{\large 2} \cdot \frac{\large \sin \beta}{\large 1+\cos \beta} .\) | (9) |
Пример 2. Известны основание \( \small a=15 \) и \( \small \beta=30° \) равнобедренного треугольника. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанный в треугольник воспользуемся формулой (8) (или (9)). Подставим значения \( \small a=15, \; \beta=30° \) в (8):
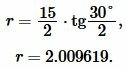 |
Ответ: 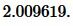
Пусть известны боковая сторона b и угол при основании β равнобедренного треугольника (Рис.3). Найдем формулу радиуса вписанной в треугольник окружности.
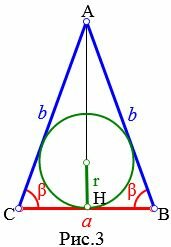 |
Высота равнобедренного треугольника AH делит равнобедренный треугольник ABC на две равные части. Тогда для треугольника AHC справедливо равенство:
| \( \small \frac{\large CH}{\large AC}=\frac{\large \frac{a}{2}}{\large b}= \cos \beta .\) |
Откуда:
| \( \small a=2b \cdot \cos \beta .\) | (10) |
Подставляя (10) в (8), получим формулу вписанной в равнобедренный треугольник окружности:
| \( \small r=\frac{\large a}{\large 2} \cdot \mathrm{tg}\frac{\large \beta}{\large 2}=\frac{\large 2b \cdot \cos \beta}{\large 2} \cdot \mathrm{tg}\frac{\large \beta}{\large 2} \) \( \small =b \cos \beta \cdot \mathrm{tg}\frac{\large \beta}{\large 2} \) |
или
| \( \small r=b \cdot \cos \beta \cdot \mathrm{tg}\frac{\large \beta}{\large 2} \) | (11) |
Учитывая формулы половинного угла тригонометрических функций, формулу (11) можно записать и так:
| \( \small r=b \cdot \frac{\large \sin \beta \ \cdot \ \cos \beta}{\large 1+ \cos \beta} \) | (12) |
Пример 3. Известны боковая сторона равнобедренного треугольника: \( \small b=9 \) и угол при основании β=35°. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (11) (или (12)).
Подставим значения \( \small b=9 ,\; \beta=35° \) в (11):
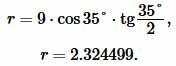 |
Ответ: 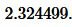
Пусть известны боковая сторона b и высота h равнобедренного треугольника (Рис.4). Найдем формулу радиуса вписанной в треугольник окружности.
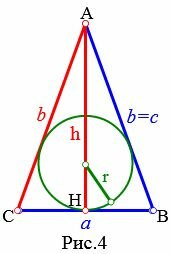 |
Формула радиуса вписанной окружности через площадь и полупериметр имеет следующий вид (см. статью на странице Радиус вписанной в треугольник окружности онлайн) :
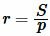 , , |
(13) |
где
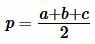 |
(14) |
Так как треугольник AHC прямоугольный, то из Теоремы Пифагора имеем:
| \( \small \left( \frac{\large a}{\large 2}\right)^2=b^2-h^2 \) |
Откуда
| \( \small a=2 \cdot \sqrt{b^2-h^2} \) | (15) |
Площадь равнобедренного треугольника по основанию и высоте вычисляется из формулы:
| \( \small S=\frac{\large 1}{\large 2} \cdot a \cdot h. \) | (16) |
Подставим (15) в (16):
| \( \small S=h \cdot \sqrt{b^2-h^2} \) | (17) |
Учитывая, что для равнобедренного треугольника b=c, а также равенство (15), получим:
| \( \small p=\frac{\large a+b+c}{\large 2} \) \( \small =\frac{\large a+2b}{\large 2} \) \( \small =\frac{\large a}{\large 2}+b \)\( \small =b+ \sqrt{b^2-h^2} \) | (18) |
Подставляя, наконец, (17) и (18) в (13), получим формулу радиуса вписанной в равнобедренный треугольник окружности:
| \( \small r=\frac{\large S}{\large p} \) \( \small =\frac{\large h \cdot \sqrt{b^2-h^2}}{\large b+ \sqrt{b^2-h^2}} \) | (19) |
Пример 4. Боковая сторона и высота равнобедренного треугольника равны \( \small b=7 ,\) \( \small h=5, \) соответственно. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в равнобедренный треугольник воспользуемся формулой (19). Подставим значения \( \small b=7 ,\) \( \small h=5 \) в (19):
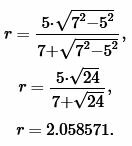 |
Ответ: 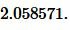
Пусть известны основание a и высота h равнобедренного треугольника (Рис.5). Найдем формулу радиуса вписанной в равнобедренный треугольник окружности.
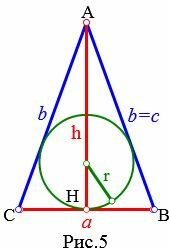 |
Из формулы (15) найдем b:
| \( \small b^2-h^2=\left( \frac{\large a}{\large 2} \right)^2 \) |
| \( \small b^2= \frac{\large a^2}{\large 4} +h^2 \) |
| \( \small b= \frac{\large 1}{\large 2} \cdot \sqrt{ a^2+ 4h^2 }\) | (20) |
Подставляя (20) в (19), получим формулу радиуса вписанной окружности в равнобедренный треугольник:
| \( \small r=\frac{\large h \cdot \sqrt{b^2-h^2}}{\large b+ \sqrt{b^2-h^2}}\) \( \small =\frac{\large h \cdot \sqrt{\frac{\large a^2}{\large 4}+h^2-h^2}}{\large \frac{\large 1}{\large 2} \cdot \sqrt{ a^2+ 4h^2 }+ \sqrt{\frac{\large a^2}{\large 4}+h^2-h^2}}\) \( \small = \large \frac{ h \ \cdot \ \frac{ a}{ 2}}{ \frac{ 1}{ 2} \cdot \sqrt{ a^2+ 4h^2 }+\frac{ a}{ 2} }\) |
или
| \( \small r=\large \frac{ a \cdot h }{a+ \sqrt{ a^2+ 4h^2 }}\) | (21) |
Пример 5. Основание и высота равнобедренного треугольника равны \( \small a=7 ,\) \( \small h=9, \) соответственно. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в равнобедренный треугольник воспользуемся формулой (21). Подставим значения \( \small a=7 ,\) \( \small h=9 \) в (21):
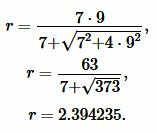 |
Ответ: 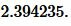
Смотрите также: