Прямая − одно из фундаментальных понятий евклидовой геометрии.
Прямая не может быть определена в терминах ранее определенных объектов.
Прамая бесконечна, она не имеет ни начала ни конца.
Прямая обычно обозначается маленькой латинской буквой. Прямую можно обозначить также через две разные точки на этой прямой (Рис.1):
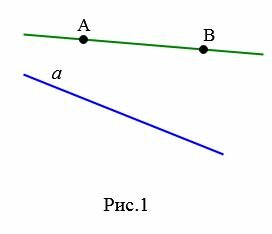 |
1. Через любую точку можно провести бесконечно много прямых.
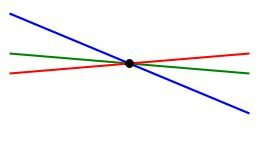 |
2. Через любые несовпадающие точки можно провести только одну прямую.
 |
3. Две несовпадающие прямые на плоскости или пересекаются, или параллельны.
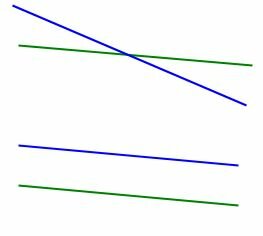 |
4. Из трех разных точек, лежащих на данной прямой, только одна может лежать между двумя другими точками.
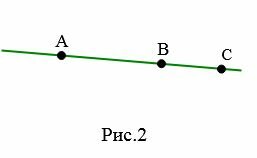 |
На Рис.2 точка B лежит между точками A и C.
Можно сказать также:
5. Есть точки, лежащие на прямой и не лежащие на ней.
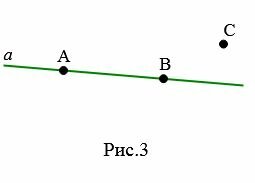 |
На Рис.3 точки A и B лежат на прямой a, а точка C не лежит на прямой a. Можно сказать также, что точки A и B принадлежат прямой a, а точка C не принадлежит прямой a. Или же прямая a проходит через точки A и B и не проходит через точку C.
Для записи принадлежности точки к прямой используют символ ∈. Запись \( \small A∈ a\) обозначает, что точка A принадлежит прямой a. Чтобы указать, что точка не принадлежит к прямой используют символ \( \small ∉. \) Запись \( \small C∉ a\) обозначает, что точка C не принадлежит прямой a.
6. В трехмерном пространстве прямые или пересекаются, или параллельные, или скрещиваются.
7. Если две любые точки прямой лежат на плоскости, то все точки этой прямой лежат на этой плоскости.
Смотрите также: