Теорема 1 Любая сторона треугольника меньше суммы двух других сторон.
Доказательство. Рассмотрим произвольный треугольник ABC (Рис.1).
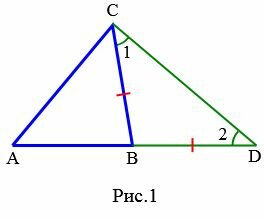 |
Докажем, что \( \small AC \lt AB+BC .\) На продолжении стороны AB отложим отрезок BD равный стороне BC. Полученный треугольник BCD равнобедренный. тогда \( \small \angle 1= \angle 2.\) Рассмотрим треугольник ADC. В этом треугольнике \( \small \angle ACD \gt \angle 1 \) и учитывая, что \( \small \angle 1= \angle 2, \) получим \( \small \angle ACD \gt \angle 2. \) По теореме 1 статьи Соотношения между сторонами и углами треугольника, против большего угла треугольника лежит большая сторона. Следовательно в треугольнике ADC имеет место неравенство:
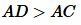 . . |
(1) |
Но
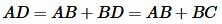 . . |
(2) |
Тогда из (1) и (2) получим:
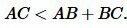  |
Следствие 1. Для любых точек A, B, C, не расположенных на одной прямой справедливы следующие неравенства:
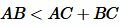 , , 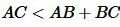 , , 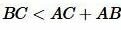 . . |
(3) |
Неравенства (3) называются неравенствами треугольника.