С помощю этого онлайн калькулятора можно найти площадь квадрата. Для нахождения площади квадрата, введите известные данные в ячейку и нажмите на кнопку "Вычислить". Теоретическую часть и численные примеры смотрите ниже.
Определение 1. Площадь квадрата − это величина той части плоскости, которую занимает квадрат.
За единицу измерения площадей применяют квадрат, сторона которого равна единице измерения отрезков. В качестве единицы измерения площадей принимают квадраты со сторонами 1мм, 1см, 1дм, 1м и т.д (Рис.1). Такие квадраты назыают квадратным миллиметром, квадратным сантиметром, квадратным дециметром, квадратным метром и т.д., соответственно. Обозначаются они мм2, см2, дм2, м2 и т.д., соответственно.
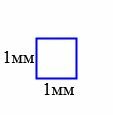 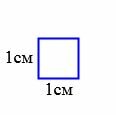 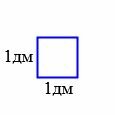 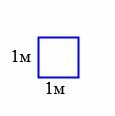 |
| Рис.1 |
Если выбрана единица измерения, то площадь измеряемого объекта (квадрата, треугольника, прямоугольника, многоугольника и т.д.)определяется положительным числом, которая определяет сколько раз единица измерения и ее части укладываются в данном объекте.
Для измерения отдельных плоских фигур используются специальные формулы. В данной статье мы выведем формулу для вычисления площади квадрата.
Теорема 1. Площадь S квадрата со стороной a равна 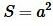 .
.
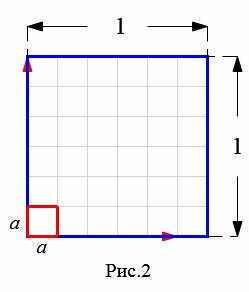 |
Доказательство. Пусть n целое неотрицательное число и пусть 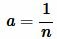 . Рассмотрим квадрат со стороной 1 (Рис.2). Разделим этот квадрат по ветрикали и по горизонлали на n равных частей. Получим
. Рассмотрим квадрат со стороной 1 (Рис.2). Разделим этот квадрат по ветрикали и по горизонлали на n равных частей. Получим 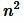 маленьких квадратов состоронами
маленьких квадратов состоронами 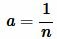 . Поскольку площадь большого квадрата равна 1 (так как является единицей измерения), то очевидно, что площадь маленького квадрата равна:
. Поскольку площадь большого квадрата равна 1 (так как является единицей измерения), то очевидно, что площадь маленького квадрата равна:
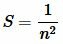 |
а поскольку 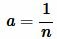 , то имеем:
, то имеем:
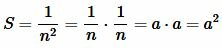 . . |
(1) |
Пусть теперь a является конечной десятичной дробью, содержащую n знаков после запятой. (Если n=0, то a будет целым числом). Тогда a можно представить в виде обыкновенной дроби, умножив и делив на 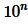 :
:
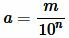 , , |
откуда
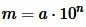 , , |
(2) |
где m − целое число.
Возьмем квадрат со стороной a и разделим его по горизонлали и вертикали на m ровных частей. Получим m2 маленьких квадратов (Рис.3).
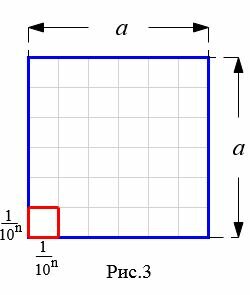 |
Тогда, учитывая (2), сторона каждого квадрата равна:
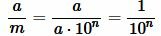 |
По формуле (1) площадь маленького квадрата равна:
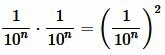 |
Следовательно, площадь квадрата со стороной a равна:
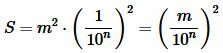 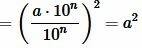 |
(3) |
Пусть, далее, число a представляет собой бесконечную десятичную дробь. Рассмотрим число an которая получается из a отбрасыванием всех десятичных знаков после запятой, начиная с (n+1)-го. Поскольку a отличается от an не более, чем на 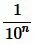 , то имеем:
, то имеем:
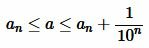 , , |
откуда
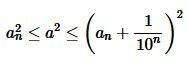 . . |
(4) |
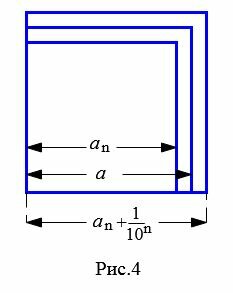 |
Из неравенства (4) следует, что площадь S квадрата со стороной a заключена между площадью квадрата со стороной an и площадью квадрата со стороной 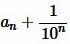 (Рис.4), т.е.
(Рис.4), т.е.
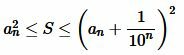 . . |
(5) |
При неограниченном увеличении числа n, число 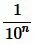 будет становиться сколь угодно малым и, следовательно, число
будет становиться сколь угодно малым и, следовательно, число 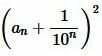 будет сколь угодно мало отличаться от
будет сколь угодно мало отличаться от 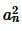 . Тогда из неравенства (5) следует, что число S будет мало отличаться от числа
. Тогда из неравенства (5) следует, что число S будет мало отличаться от числа 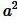 . Следовательно они равны, т.е.
. Следовательно они равны, т.е. 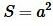 .
.
Из вышеизложенного доказательства получили, что площадь квадрата равна:
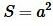 . . |
(6) |
где \( \small a \) сторона квадрата.
Пример 1. Сторона квадрата равна 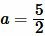 . Найти площадь квадрата.
. Найти площадь квадрата.
Решение. Для нахождения плошади квадрата воспользуемся формулой (6). Подставляя 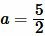 в (6), получим:
в (6), получим:
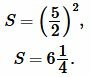 |
Ответ: 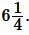
Пусть известна диагональ \( \small d \) квадрата (Рис.5). Найдем площадь квадрата.
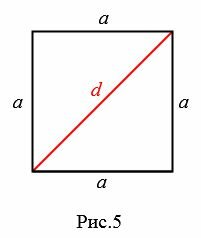 |
Для нахождения плошади квадрата, найдем сначала сторону \( \small a \) квадрата. Для этого воспользуемся теоремой Пифагора:
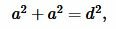 |
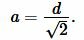 |
(7) |
Подставляя (7) в (6), получим:
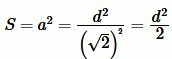 |
то есть площадь квадрата по диагонали вычисляется из следующей формулы:
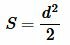 . . |
(8) |
Пример 2. Диагональ квадрата равна 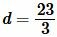 . Найти площадь квадрата.
. Найти площадь квадрата.
Решение. Для нахождения плошади квадрата воспользуемся формулой (8). Подставляя 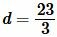 в (8), получим:
в (8), получим:
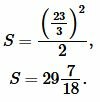 |
Ответ: 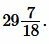
Пусть известен \( \small r \) радиус окружности вписанной в квадрат (Рис.6). Найдем площадь квадрата.
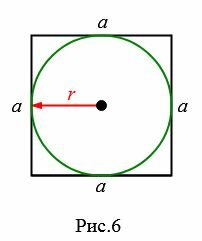 |
Для нахождения плошади квадрата, найдем сначала сторону \( \small a \) квадрата. Нетрудно заметить, что радиус \( \small r \) равна половине стороны \( \small a \) квадрата, т.е.
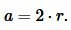 |
(9) |
Подставляя (9) в (6), получим:
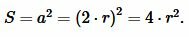 |
или
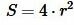 . . |
(10) |
Пример 3. Радиус вписанной в квадрат окружности равен 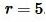 . Найти площадь квадрата.
. Найти площадь квадрата.
Решение. Для нахождения плошади квадрата воспользуемся формулой (10). Подставляя 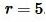 в (10), получим:
в (10), получим:
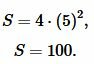 |
Ответ: 
Пусть известен \( \small R \) радиус окружности описанной около квадрата (Рис.7). Найдем площадь квадрата.
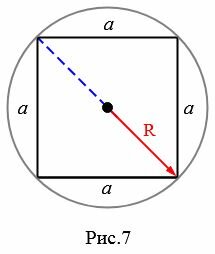 |
Для нахождения плошади квадрата, найдем сначала сторону \( \small a \) квадрата. Восрользуемся теоремой Пифагора:
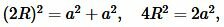 |
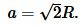 |
(11) |
Подставляя (11) в (6), получим:
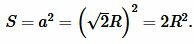 |
(12) |
Пример 4. Радиус описанной окружности равен 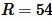 . Найти площадь квадрата.
. Найти площадь квадрата.
Решение. Для нахождения площади квадрата воспользуемся формулой (12). Подставляя 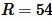 в (12), получим:
в (12), получим:
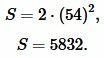 |
Ответ: 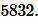
Пусть известен периметр \( \small P \) квадрата. Найдем площадь квадрата. По периметру можно найти сторону квадрата:
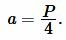 |
(13) |
Подставляя (13) в (6), получим:
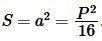 |
то есть площадь квадрата через периметр равна:
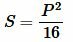 |
(14) |
Пример 5. Периметр квадрата равен 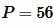 . Найти площадь квадрата.
. Найти площадь квадрата.
Решение. Для нахождения площади квадрата воспользуемся формулой (14). Подставляя 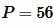 в (14), получим:
в (14), получим:
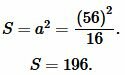 |
Ответ: 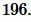
Смотрите также: