Теорема 1 (Теорема Фалеса). Пусть через точки \( \small A, \ B, \ C, D \) расположенные на одной стороне угла проведены параллельные прямые, которые пересекают другую сторону этого угла в точках \( \small A_1, \ B_1, \ C_1, D_1, \) соответственно. Тогда если равны отрезки \( \small AB \) и \( \small CD, \) то равны и отрезки \( \small A_1B_1 \) и \( \small C_1D_1. \)
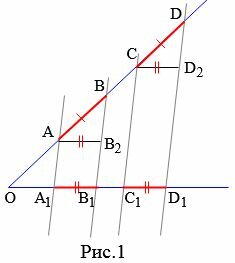 |
Доказательство. Пусть \( \small AB=CD \) и пусть прямые \( \small AA_1, \ BB_1, \ CC_1, DD_1 \) параллельны (Рис.1). Докажем, что \( \small A_1B_1=C_1D_1. \) Проведем прямые \( \small AB_2 \) и \( \small CD_2 \) параллельно стороне \( \small OD_1. \) Получили два четырехугольника \( \small AB_2B_1A_1 \) и \( \small CD_2D_1C_1. \) Эти четырехугольники являются параллелограммами поскольку противоположные стороны этих четырехугольников параллельны. Тогда
| \( \small AB_2=A_1B_1, \) \( \small CD_2=C_1D_1. \) | (1) |
Углы \( \small BAB_2 \) и \( \small DCD_2 \) являются соответствующими углами при пересечении параллельных прямых \( \small AB_2 \) и \( \small CD_2 \) секущей \( \small AD \) (см. статью Теоремы об углах, образованных двумя параллельными прямыми и секущей). Тогда
| \( \small ∠BAB_2=∠DCD_2. \) | (2) |
Углы \( \small ABB_2 \) и \( \small CDD_2 \) являются соответствующими углами при пересечении параллельных прямых \( \small BB_2 \) и \( \small DD_2 \) секущей \( \small AD. \) Тогда
| \( \small ∠ABB_2=∠CDD_2. \) | (3) |
Треугольники \( \small ABB_2 \) и \( \small CDD_2 \) равны по второму признаку равенства треугольников так как \( \small AB=CD \) и выполнены равенства (2) и (3). Следовательно \( \small AB_2 = CD_2. \) Отсюда, учитывая (1) получим: \( \small A_1B_1=C_1D_1. \) Теорема доказана.