С помощю этого онлайн калькулятора можно найти радиус описанной окружности около любого треугольника. Для нахождения радиуса окружности описанной около треугольника введите известные данные в ячейки и нажмите на кнопку "Вычислить". Теоретическую часть и численные примеры смотрите ниже.
Пусть известны основание a равнобедренного треугольника и боковая сторона b=c. Найдем радиус описанной окружности около равнобедренного треугольника. На странице Радиус окружности описанной около треугольника онлайн была выведена формула вычисления радиуса R описанной около любого треугольника окружности:
| \( \small R=\frac{\large abc}{\large 4\ \cdot \ \sqrt{p(p-a)(p-b)(p-c)}}. \) | (1) |
где p вычисляется из формулы:
| \( \small p= \frac{\large a+b+c}{\large 2}. \) | (2) |
Учитывая, что у нас треугольник равнобедренный, т.е. b=c, имеем:
| \( \small p= \frac{\large a+2b}{\large 2}=b+ \frac{ \large a}{ \large 2}, \) | (3) |
| \( \small p-a= b- \frac{ \large a}{ \large 2}, \) | (4) |
| \( \small p-b= \frac{ \large a}{ \large 2}, \) | (5) |
Подставляя (3)−(5) в (1) и учитывая, что b=c, получим:
| \( \small R=\frac{\large ab^2}{\large 4\ \cdot \frac{a}{2} \cdot \sqrt{\left ( b+\frac{a}{2}\right)\left ( b-\frac{a}{2}\right)}} \) \( \small =\frac{\large b^2}{\large 2 \ \cdot \ \sqrt{ b^2-\frac{a^2}{4}}} \) \( \small =\frac{\large b^2}{ \sqrt{ \large 4b^2-a^2}} ,\) |
то есть
| \( \small R=\frac{\large b^2}{ \sqrt{ \large 4b^2-a^2}}. \) | (6) |
Пример 1. Известны основание \( \small a=7 \) и боковая сторона \( \small b=\frac{9}{2} \) равнобедренного треугольника. Найти радиус окружности описанной около треугольника.
Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (6).
Подставим значения \( \small a=7 \) и \( \small b=\frac{9}{2} \) в (6):
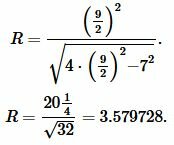 |
Ответ: 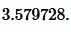
Пусть известны сторона a и противолежащий угол A. Формула для нахождения радиуса окружности описанной около равнобедренного треугольника по основанию и противолежащему углу аналогична формуле для нахождения радиуса окружности описанной около произвольного треугольника:
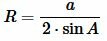 . . |
(7) |
Пример 2. Сторона основание равнобедренного треугольника равна:\( \small a=21 \) а противолежащий угол \( \small \angle A=60°.\) Найти радиус окружности описанной около треугольника.
Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (7). Подставим значения \( \small a=21 \) и \( \small \angle A=60° \) в (7):
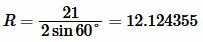 . . |
Ответ: 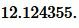
Пусть известны боковая сторона b=c равнобедренного треугольника и угол между боковыми сторонами A. Найдем радиус описанной окружности около равнобедренного треугольника.
На странице Радиус описанной окружности около треугольника онлайн была выведена формула для нахождения радиуса описанной окружности около треугольника при известных сторонах и углу между ними:
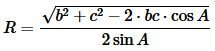 . . |
(8) |
Подставляя в (8) c=b, получим:
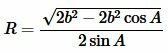 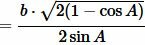 |
то есть
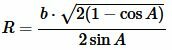 . . |
(9) |
Пример 3. Известны основание \( \small a=21 \) равнобедренного треугольника и угол между боковыми сторонами: \( \small \angle A=70°. \) Найти радиус окружности описанной около треугольника.
Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (9). Подставим значения \( \small a=21; \) и \( \small \angle A=70° \) в (9):
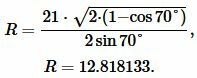 |
Ответ: 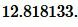
Пусть известны основание a равнобедренного треугольника и прилежащие к ней угол B=C. Найдем радиус описанной окружности около треугольника. На странице Радиус описанной окружности около треугольника онлайн была выведена формула для нахождения радиуса описанной окружности около треугольника при известной стороне и прилежащим двум углам:
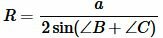 . . |
(10) |
Подставляя \( \small C=B \) в (10), получим требуемую формулу:
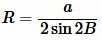 . . |
(11) |
Пример 4. Известны основание равнобедренного треугольника \( \small a=14 \) и прилежащий к ней угол: \( \small \angle B=25°. \) Найти радиус окружности описанной около треугольника.
Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (11). Подставим значения \( \small a=14 \) и \( \small \angle B=25° \) в (11):
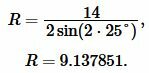 |
Ответ: 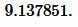
Смотрите также: