Определение 1. Средней линией треугольника называется отрезок, соединяющий середины двух сторон.
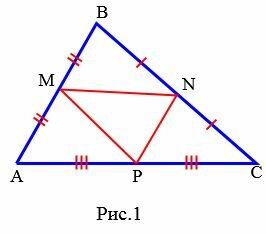 |
У треугольника три средние линии. На Рис.1 отрезки MN, NP, MP являются средними линиями треугольника.
Теорема 1. Средняя линия треугольника, соединяющая середины двух его сторон параллельна третьей стороне и равна ее половине.
Доказательство. Пусть MN средняя линия треугольника ABC (Рис.2). Докажем, что \( \small MN || AC, \) \( \small MN=\frac12 AC. \)
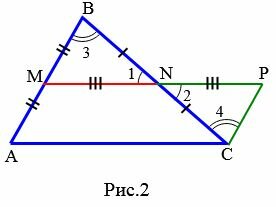 |
Через отрезок MN проведем прямую и отметим на ней точку P так, что \( \small MN=NP. \) Имеем: \( \small BN=NC \) поскольку N является серединой отрезка BC. Так как углы 1 и 2 вертикальные, то \( \small \angle 1=\angle 2. \) Тогда, учитывая также \( \small MN=NP \) получим, что треугольники MBN и NPC равны по первому признаку равенства треугольников. Отсюда имеем: \( \small \angle 3=\angle 4 \) и MB = CP. Но углы 3 и 4 накрест лежащие, при рассмотрении прямых AB и CP пересеченных секущей BC и, учитывая, что \( \small \angle 3=\angle 4. \) (теорема 1 статьи Параллельные прямые. Признаки параллельности прямых) получим, что AB || CP или AM || CP .
Далее, поскольку точка M является серединой отрезка AB, имеем : AM=MB. Но \( \small MB=CP \) и, следовательно AM = CP. Получили что в четырехугольнике AMPC стороны AM и CP параллельны и равны. Тогда по признаку 1 статьи Параллелограмм четырехугольник AMPC является параллелограммом. Отсюда следует, что MP || AC или MN ||AC.
Остается показать, что \( \small MN=\frac12 AC. \) Так как MN=NP, то \( \small MN=\frac12 MP. \) Но в параллелограмме MP = AC. Тогда \( \small MN=\frac12 AC. \)