Определение 1. Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.
Определение 2. Сходственными называются стороны подобных треугольников, лежащих напротив равных углов.
 |
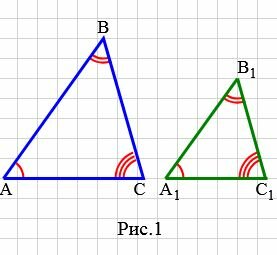На рисунке 1 углы треугольников \( \small ABC \) и \( \small A_1B_1C_1 \) соответственно равны:
  |
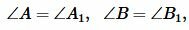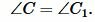(1) |
Тогда стороны \( \small AB \) и \( \small A_1B_1 \), \( \small BC \) и \( \small B_1C_1 \), \( \small AC \) и \( \small A_1C_1 \) называются сходственными.
Определение 1 можно понимать так: два треугольника подобны, если для них можно ввести обозначения 
и 
(Рис.1) так, что
  |
 . |
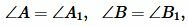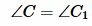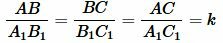(2) |
Если два треугольника и подобны, то это обозначают так:
 . |
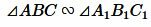Коэффициентом подобия треугольников k − это число, равное отношению сходственных сторон (см. формулу (2)).
Теорема 1. Если два угла одного треугольника соответсвенно равны двум углам другого треугольника, то такие треугольники подобны.
 |
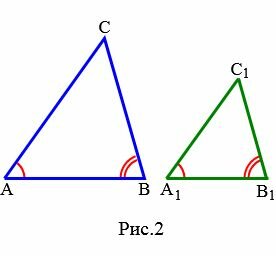Доказательство. Пусть заданы два треугольника и и пусть 
, 
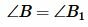. Докажем, что 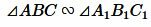(Рис.2).
Поскольку сумма углов треугольника равна 180°, то можно записать:
 ,  |
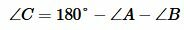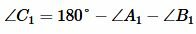и, так как , , 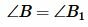получим:
 . |
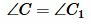Таким образом углы треугольника соответственно равны углам треугольника . Покажем, теперь, что стороны одного треугольника пропорциональны сходственным сторонам другого треугольника, т. е. выполнено равенство (2).
Площади треугольников и по двум сторонам и углу между ними можно вычислить формулами:
 , |
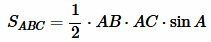(3) |
 . |
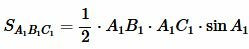(4) |
Из (3) и (4), и из следует:
 . |
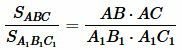(5) |
С другой стороны:
 , |
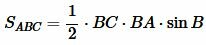(6) |
 . |
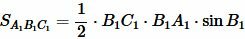(7) |
Из (6) и (7), и из 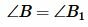следует:
 . |
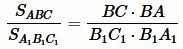(8) |
Левые части уравнения (5) и (8) равны. Следовательно равны и правые части:
 . |
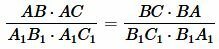(9) |
Умножая левую и правую части уравнения (9) на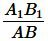 
, получим:
 . |
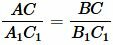(10) |
Продолжая аналогичные рассуждения, получим:
 . |
 . |
 . |
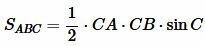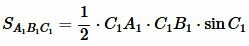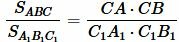(11) |
Сравнивая (8) и (11), получим:
 . |
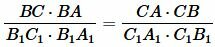(12) |
Умножая левую и правую части уравнения (12) на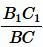 
, получим:
 . |
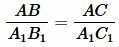(13) |
Из (10) и (13), получим:
 . |
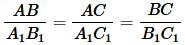(14) |
То есть стороны треугольника пропорциональны сходственным сторонам треугольника . Что и требовалось доказать.
Теорема 2. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы между этими сторонами равны, то такие треугольники подобны.
 |
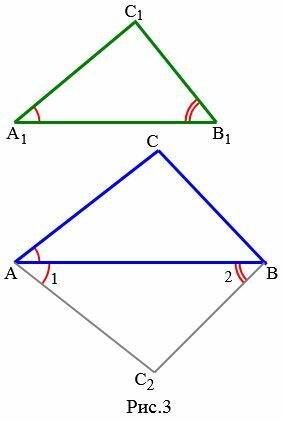Доказательство. Пусть заданы два треугольника и и пусть , 
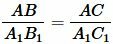. Докажем, что 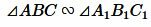(Рис.3).
Рассмотрим треугольник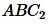 
у которого
 ,  . |
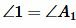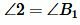(15) |
Из условия (15) следует, что треугольники 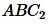и подобны (по первому признаку подобия треугольников). Следовательно:
 . |
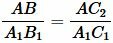Но по условию теоремы 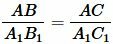. Поэтому 
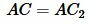. Треугольники 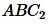и равны по двум сторонам и углу между ними (сторона AB общая, ,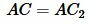 
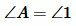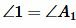(поскольку и )). Следовательно 
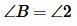и поскольку 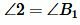, то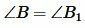 
.
Получили, что и 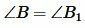. Тогда по первому признаку подобия треугольников .
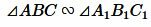Теорема 3. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Доказательство. Пусть стороны треугольников пропорциональны:
| . |
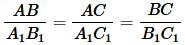(16) |
Докажем, что 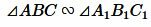. Рассотрим треугольник 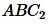у которого 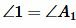, 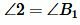(Рис.3). Треугольники 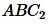и подобны по первому признаку подобия треугольников. Тогда выполнено следующее равенство:
 . |
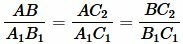(17) |
Сравнивая равенства (16) и (17) получаем: ,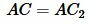 
.
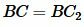Из этих рассуждений следует, что треугольники 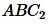и равны по трем сторонам (см. статью Треугольники. Признаки равенства треугольников). Тогда 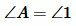, а поскольку 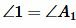, то . Следовательно, по второму признаку подобия треугольников, треугольники и подобны: .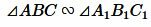
Теорема 4. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Доказательство. Пусть треугольники и подобны. Тогда
| . |
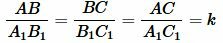и
| , . |
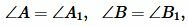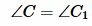где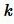 
-коэффициент подобия.
Площади треугольников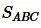 
и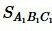 
по двум сторонам и углу между ними равны:
 , |
 . |
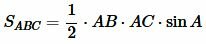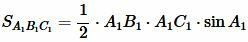Тогда
  . |
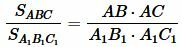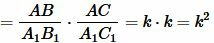