Определение 1. Ломаной (ломаной линией) \( \small A_1A_2...A_{n-1}A_n \) называется геометрическая фигура, которая состоит из \( \small [ A_1A_2 ],\) \( \small [ A_2A_3 ],...,\) \( \small [ A_{n-1}A_n ]\) последовательно соединенных своими концами отрезков и никакие последовательные две отрезки\( \small [ A_{k}A_{k+1} ]\) и \( \small [ A_{k+1}A_{k+2} ]\) при \( \small k=1,2,...,n-2 \) не лежат на одной прямой.
Можно дать и другое определение ломаной:
Определение 2. Если \( \small A_1, \ A_2, ..., \ A_n \) различные точки, никакие проследовательные три из которых не лежат на одной прямой, то совокупность отрезков \( \small [ A_1A_2 ],\) \( \small [ A_2A_3 ],...,\) \( \small [ A_{n-1}A_n ]\) называется ломаной или ломаной линией.
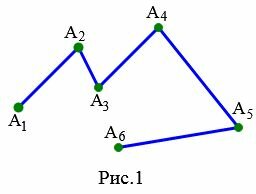
На рисунке 1 изображена ломаная состоящая из пяти отрезков \( \small [ A_1A_2 ]\) , \( \small [ A_2A_3 ]\), \( \small [ A_3A_4 ]\), \( \small [ A_4A_5 ]\), \( \small [ A_5A_6 ]\), которые последовательно соединены своими концами.
 |
Ломаная, описанная в определении 1 называется невырожденной ломаной.
На рисунке 1 ломаная \( \small A_1A_2A_3A_4A_5A_6 \) является невырожденной поскольку отрезки \( \small [ A_1A_2 ]\) и \( \small [ A_2A_3 ]\), \( \small [ A_2A_3 ]\) и \( \small [ A_3A_4 ]\), \( \small [ A_3A_4 ]\) и \( \small [ A_4A_5 ]\), \( \small [ A_4A_5 ]\) и \( \small [ A_5A_6 ]\) не лежат на одной прямой.
Определение 3. Если \( \small A_1, \ A_2, ..., \ A_n \) различные точки, и среди них существуют проследовательные три точки, лежащие на одной прямой, то совокупность отрезков \( \small [ A_1A_2 ],\) \( \small [ A_2A_3 ],...,\) \( \small [ A_{n-1}A_n ]\) называется вырожденной ломаной или вырожденной ломаной линией.
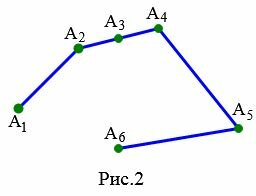 |
На рисунке 2 изображена ломаная \( \small A_1A_2A_3A_4A_5A_6 \). Эта ломаная является вырожденной поскольку отрезки \( \small [ A_2A_3 ]\) и \( \small [ A_3A_4 ]\) лежат на одной прямой.
Внимание! Если явно не указыается вырожденность ломаной, то подразумевается невырожденная ломаная.
Звеньями называют отрезки, из которых состоит ломаная.
Ломаная \( \small A_1A_2A_3A_4A_5A_6 \), изображенная на рисунке 1 состоит из звеньев \( \small [ A_1A_2 ]\) , \( \small [ A_2A_3 ]\), \( \small [ A_3A_4 ]\), \( \small [ A_4A_5 ]\), \( \small [ A_5A_6 ]\).
Конечные точки звеньев ломаной называются вершинами.
На рисунке 1 изображена ломаная \( \small A_1A_2A_3A_4A_5A_6 \), состоящая из шести вершин: \( \small A_1, \ A_2, \ A_3, \ A_4, \ A_5, \ A_6 \).
Смежные звенья ломаной − это звенья имеющие общую вершину.
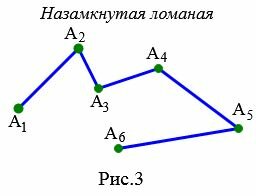
На рисунке 3 смежными звеньями ломаной \( \small A_1A_2A_3A_4A_5A_6 \) являются звенья: \( \small [ A_1A_2 ]\) и \( \small [ A_2A_3 ]\), \( \small [ A_2A_3 ]\) и \( \small [ A_3A_4 ]\), \( \small [ A_3A_4 ]\) и \( \small [ A_4A_5 ]\), \( \small [ A_4A_5 ]\) и \( \small [ A_5A_6 ]\).
Смежными вершинами ломаной называют вершины одного звена ломаной.
На рисунке 3 смежными вершинами ломаной \( \small A_1A_2A_3A_4A_5A_6 \) являются вершины: \( \small A_1\) и \( \small A_2\), \( \small A_2\) и \( \small A_3\), \( \small A_3\) и \( \small A_4 \), \( \small A_4\) и \( \small A_5\), \( \small A_5\) и \( \small A_6\).
Незамкнутым является ломаная, первая и последняя точки которой не совпадают друг с другом (Рис.3).
 |
Определение 4. Замкнутым является ломаная \( \small A_1A_2...A_{n-1}A_n \), первая \( \small A_1\) и последняя \( \small A_n \) точки которой совпадают друг с другом и отрезки \( \small A_1A_2 \) и \( \small A_{n-1}A_n \) не лежат на одной прямой.
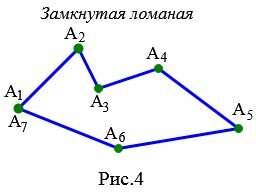 |
На рисунке 4 ломаная \( \small A_1A_2A_3A_4A_5A_6A_7 \) является замкнутым, так как точки: \( \small A_1\) и \( \small A_7\) совпадают и отрезки \( \small A_1A_2\) и \( \small A_6A_7\) не лежат на одной прямой.
Ломаная имеет самопересечение, если хотя бы два ее звена имеют общую точку, помимо общей вершины.
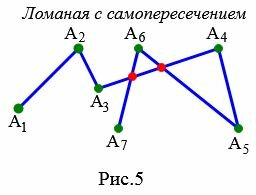 |
Ни рисунке 5 ломаная \( \small A_1A_2A_3A_4A_5A_6A_7 \) имеет самопересечение, так как звенья \( \small A_5A_6 \) и \( \small A_6A_7 \) имеют общие точки со звеном \( \small A_3A_4 \).
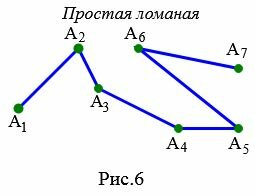
Ломаная называется простым, если не имеет самопересечений. Пример простой ломаной изображен на рисунке 6.
 |
Длина ломаной равна сумме длин всех звеньев ломаной: \( \small d= A_1A_2+A_2A_3+...+A_{n-1}A_n, \) где \( \small n \) − количество вершин ломаной.
Теорема. Длина ломаной больше расстояния между первым и последним точками.
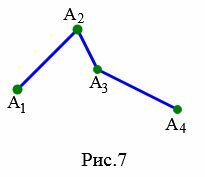 |
Доказательство. Для доказательства теоремы рассмотрим ломаную \( \small A_1A_2A_3A_4 \) с тремя звеньями (Рис.7). Так как ломаная невырождена, то вершины \( \small A_1, \ A_2, \ A_3 \) не лежат на одной прямой. Тогда имеет место неравенство треугольников:
| \( \small A_1A_2+A_2A_3 > A_1A_3 \). | (1) |
Для точек \( \small A_1, \ A_3, \ A_4 \) имеет место следующее нестрогое неравенство:
| \( \small A_1A_3+A_3A_4 ≥ A_1A_4 \). | (2) |
В выражении (2) мы не применяли строгое неравенство поскольку вершины \( \small A_1, \ A_3, \ A_4 \) ломаной не являются соседними вершинами и могут лежать на одной прямой.
В неравенстве (2) вместо слагаемого \( \small A_1 A_3\) подставим сумму \( \small A_1A_2+A_2A_3 \) из (1), которая больше, чем \( \small A_1 A_3\). Тогда получим:
| \( \small A_1A_2+A_2A_3+A_3A_4 > A_1A_4 \). |
Поседнее неравенство означает, что длина невырожденной ломаной больше расстояния между первым и последним точками.
Аналогично доказывается теорема для ломанной с любым количеством звеньев.