Теорема 1 (о соотношениях между сторонами и углами треугольника).
В треугольнике:
Доказательство. 1) Пусть задан треугольник ABC и пусть \( \small AB > AC \) (Рис.1).
 |
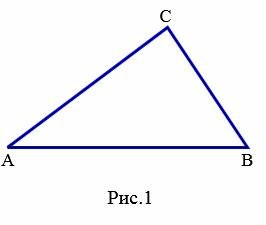Докажем, что \( \small \angle C \gt \angle B .\)
Отложим на стороне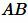 
отрезок 
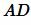, равной отрезку 
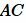(Рис.2).
 |
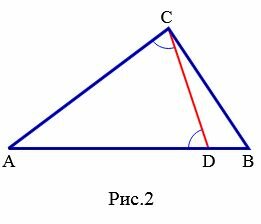Поскольку AD<AB то точка D лежит между точками A и B. Тогда угол ACD является частью угла C, т.е.:
 |
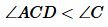(1) |
Угол ADC является внешним углом треугольника BCD. Тогда:
 |
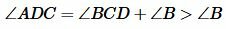(2) |
Так как AC=AD, то треугольник ACD является равнобедренным и, следовательно
 . |
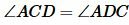(3) |
Тогда из (1), (2) и (3) следует:
  . |
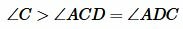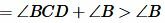или
 . |
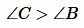Первая часть теоремы доказана.
2) Пусть в треугольнике ABC 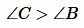. Докажем, что \( \small AB > AC. \)
Предположим обратное, т.е. 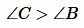но при этом \( \small AB ≯ AC. \) Это значит либо \( \small AB = AC, \) либо \( \small AB < AC. \) Если \( \small AB = AC, \) то треугольник ABC равнобедренный и, следовательно \( \small \angle C = \angle B. \) Если же \( \small AB < AC, \) то из доказательства части 1) данной теоремы следует, что \( \small \angle C \lt \angle B. \) Значит наши предположения (\( \small AB = AC \) или \( \small AB < AC \)) неверны. То есть \( \small AB > AC. \)
Следствие 1. В прямоугольном треугольнике гипотенуза больше катета.
Доказательство. В прямоугольном треугольнике напротив прямого угла (т.е. угла равного 90°) лежит гипотенуза. Остальные углы прямоугольного треугольника острые, проскольку сумма всех углов треугольника равна 180° (см. теорему статьи Сумма углов треугольника). Поскольку напротив острых углов стоят катеты и острые углы меньше 90°, то из части 2) теоремы 1 данной статьи следует, что гипотенуза больше катета.
Следствие 2 (Признак равнобедренного треугольника). Если два угла треугольника равны, то треугольник равнобедренный.
Доказательство. Пусть два угла треугольника равны. Тогда стороны лежащие напротив этих углов равны. Действительно. Если предположить, что стороны, лежащие напротив равных углов не равны, то по теореме 1, напротив большей стороны лежит большой угол, что противоречит условию следствия (что эти углы равны). Поскольку две стороны треугольника равны, то треугольник равнобедренный.