С помощю этого онлайн калькулятора можно найти радиус вписанной в любой треугольник окружности, в том числе радиус вписанной в прямоугольный треугольник окружности. Для нахождения радиуса вписанной в треугольник окружности выберите тип треугольника, введите известные данные в ячейки и нажмите на кнопку "Вычислить". Теоретическую часть и численные примеры смотрите ниже.
Пусть известны катеты a и b прямоугольного треугольника (Рис.1). Выведем формулу вычисления радиуса вписанной в треугольник окружности.
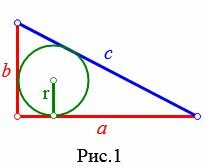 |
Радиус вписанной в треугольник окружности, если известна площадь треугольника S и полупериметр p вычисляется из следующей формулы (статья Радиус вписанной в треугольник окружности, формула (5)):
| \( \small r= \frac{\large S}{\large p}, \) | (1) |
где
| \( \small p= \frac{\large a+b+c}{\large 2}. \) | (2) |
Площадь прямоугольного треугольника по катетам вычисляется из формулы:
| \( \small S= \large \frac{1}{2} \small \cdot a \cdot b. \) | (3) |
Подставляя (2) и (3) в (1) получим формулу вписанной в прямоугольный треугольник окружности:
| \( \small r= \large \frac{\frac{1}{2}ab}{\frac{1}{2}(a+b+c)} \) \( \small = \large \frac{ab}{a+b+c}, \) | (4) |
где c вычисляется из теоремы Пифагора:
| \( \small c= \sqrt{ a^2+b^2}. \) | (5) |
Из формулы (4) выведем другую эквивалентную формулу. Умножим числитель и знаменатель формулы (4) на \( \small a+b-c \):
| \( \small r= \frac{\large ab(a+b-c)}{\large (a+b+c)(a+b-c)} \) \( \small = \frac{\large ab(a+b-c)}{\large (a+b)^2-c^2} \) \( \small = \frac{\large ab(a+b-c)}{\large a^2+2ab+b^2-c^2} \) | (6) |
Учитывая (5), формулу (6) можно переписать так:
| \( \small r= \frac{\large ab(a+b-c)}{\large 2ab} \) \( \small = \frac{\large a+b-c}{\large 2} .\) |
Таким образом другая формула вычисления радиуса вписанной в треугольник окружности имеет вид:
| \( \small r= \frac{\large a+b-c}{\large 2} ,\) | (7) |
где c вычисляется из (5).
Пример 1. Известны катеты прямоугольного треугольника a=17 и b=5. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся одним из формул (4) и (7). Вычислим, сначала, гипотенузу прямоугольного треугольника из формулы (5):
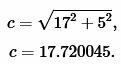 |
Подставим значения \( \small a=17, \; b=5\; c=17.720045 \) в (7):
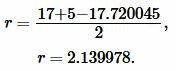 |
Ответ: 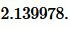
Пусть известны катет a прямоугольного треугольника и прилежащий к нему угол β(Рис.2). Выведем формулу радиуса вписанной в треугольник окружности.
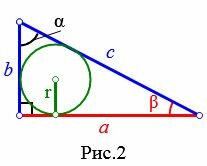 |
Из теоремы синусов имеем:
| \( \small \frac{\large a}{\large \sin \alpha}=\frac{\large b}{\large \sin \beta} .\) |
Учитывая, что \( \small \alpha=90°-\beta \) и \( \small \sin \ (90°-\beta)=\cos \beta \), получим:
| \( \small \frac{\large a}{\large \sin \alpha}=\frac{\large a}{\large \sin (90°-\beta)} \) \( \small =\frac{\large a}{\large \cos \beta}=\frac{\large b}{\large \sin \beta} .\) | (8) |
Тогда из (8) получим:
| \( \small b=\frac{\large a \cdot \sin \beta}{\large \cos \beta}. \) | (9) |
Далее, из теоремы синусов:
| \( \small \frac{\large a}{\large \sin \alpha}=\frac{\large a}{\large \sin (90°-\beta)} \) \( \small =\frac{\large a}{\large \cos \beta}=\frac{\large c}{\large \sin 90°} .\) |
Откуда:
| \( \small c=\frac{\large a}{\large \cos \beta} .\) | (10) |
Чтобы получить формулу радиуса вписанной в прямоугольный треугольник окружности через катет и прилежащий к нему угол, подставим значения \( \small b \) и \( \small c \) из (9) и (10) в (7):
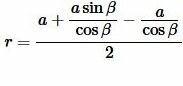 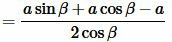 |
или
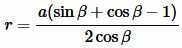 |
(11) |
Пример 2. Известны катет \( \small a=21 \) и прилежащий к нему угол \( \small \beta=30° \) прямоугольного треугольника. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (11). Подставим значения \( \small a=21 \) \( \small \beta=30° \) в (11):
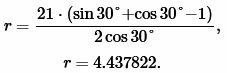 |
Ответ: 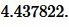
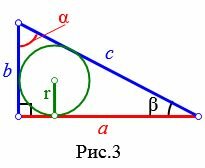
Пусть известны катет a прямоугольного треугольника и противолежащий угол \( \small \alpha; \) (Рис.3). Найдем формулу радиуса вписанной в треугольник окружности.
 |
В предыдущем параграфе мы вывели формулу вписанной в прямоугольный треугольник окружности по катету и прилежащему углу (формула (11)). Учитывая, что в прямоугольном треугольнике сумма острых углов равна 90°, имеем:
| \( \small \alpha+\beta=90°\) \( \small \beta=90°-\alpha \) |
Тогда (11) можно преобразовать так (подробнее на странице Формулы приведения тригонометрических функций:
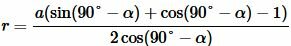 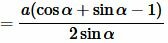 |
или
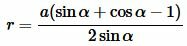 |
(12) |
Пример 3. Известны катет \( \small a=6 \) прямоугольного треугольника и противолежащий угол \( \small \alpha=53°. \) Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (12). Подставим значение \( \small a=6, \; \alpha=53° \) в (12):
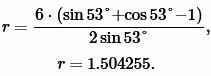 |
Ответ: 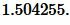
Смотрите также: