Четырехугольник, вписанный в окружность

Определение 1. Четырехугольник называют вписанным в окружность, если все вершины четырехугольника лежат на окружности.

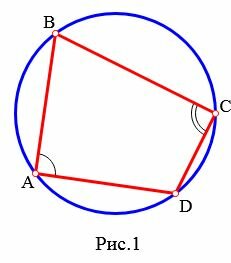
На рисунке 1 четырехугольник ABCD вписан в окружность. В этом случае говорят также, что окружность описан около четырехугольника.

Теорема 1. Если четырехугольник вписан в окружность, то сумма противолежащих углов четырехугольника равна 180°.

Доказательство. Пусть четырехугольник ABCD вписан в окружность (Рис.1). Докажем, что .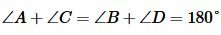

Углы A и C являются вписанными. Следовательно:

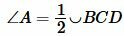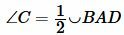Но 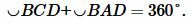Следовательно

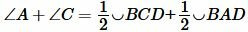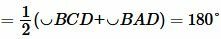Аналогично можно показать, что .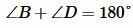

Заметим, что из 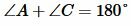следует 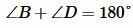, поскольку сумма углов четырехугольника равна 360°.

Как известно, вокруг любого треугольника можно описать окружность (см. статью Окружность, описанная около треугольника). Однако вокруг не каждого четырехугольника можно описать окружность. Например, если параллелограмм не является прямоугольником, то вокруг него не возможно описать окружность. Следующая теорема позволяет распознать четрехугольники, вокруг которых можно описать окружность.

Теорема 2. Если в четырехугольнике сумма противолежащих углов равна 180°, то около него можно описать окружность.

Доказательство. Пусть задан четырехугольник ABCD и пусть 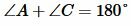. Докажем, что около него можно описать окружность.

Предположим, что около этого четырехугольника невозможно описать окружность. Рассмотрим треугольник ABD и опишем окружность около этого треугольника (как отметили выше около любого треугольника можно описать окружность). Поскольку мы предположили, что у этого четырехугольника невозможно описать окружность, то точка C не принадлежит этой окружности. Поэтому эта точка лежит вне окружности или находится внутри окружности.

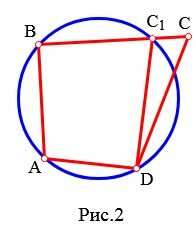Случай 1. Точка C лежит вне описанной окружности (Рис.2).

Тогда сторона BC пересекает этот окружность. Обозначим эту точку C₁. Четырехугольник ABC₁D вписан в окружность. Тогда по теореме 1 имеем: 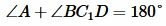. Но по условию теоремы 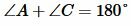. Следовательно 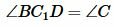. С другой стороны, угол BC₁D является внешним углом треугольника DC₁C, т.е. выполняется равенство 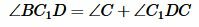. Получили противоречие, следовательно точка C не может лежать вне окружности.

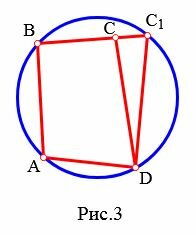
Случай 2. Точка C лежит внутри описанной окружности (Рис.3).

Проведем прямую BC и точку пересечения прямой и окружности обозначим C₁. Получили четырехугольник ABC₁D вписанный в окружность. Тогда по теореме 1 имеем: 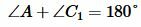. Но по условию данной теоремы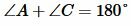. Следовательно, .

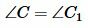С другой стороны, угол C (т.е. угол BCD) является внешним углом треугольника DC₁C, т.е. выполняется равенство 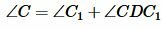. Получили противоречие, следовательно точка C не может лежать внутри окружности.

Следовательно точка C лежит на окружности.

Теорема 2 можно рассматривать метод определения принадлежности четырех точек одной окружности. Если четырехугольник вписан в окружность, то существует точка, равноудаленная от всех вершин четырехугольника (это центр окружности). Чтобы найти эту точку достаточно построить серединные перпендикуляры двух соседних сторон четырехугольника и найти точку их пересечения.