

В данной статье мы рассмотрим каноническое уравнение прямой на плоскости. Определим понятие направляющего вектора прямой. Рассмотрим примеры построения канонического уравнения прямой, если известны две точки этой прямой или если известна одна точка и направляющий вектор этой прямой. Представим метод преобразования уравнения в каноническом виде в параметрический и общий виды.
Определение 1. Любой ненулевой вектор, параллельный данной прямой называется направляющим вектором этой прямой.
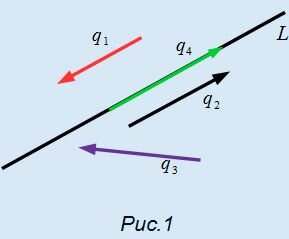 |
На рисунке Рис.1 представлена прямая L и векторы q1, q2, q3, q4. Из определения следует, что векторы q1, q2, q4 являются направляющими векторами прямой L, а q3 − нет.
Каноническое уравнение прямой L на плоскости представляется следующей формулой:
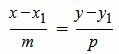 |
(1) |
где x1, y1 координаты некоторой точки M1 на прямой L. Вектор q={m, p} является направляющим вектором прямой L.
Надо отметить, что при записи уравнения прямой в каноническом виде, допускается, чтобы один из чисел m и p была равна нулю (одновременно m и p не могут быть равным нулю, т.к. направляющий вектор прямой не должен быть нулевым вектором). Равенство нулю одного из знаменателей означает равенство нулю соответствующего числителя. В этом можно убедится, записав уравнение (1) в следующем виде:
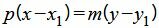 . . |
(2) |
Пусть в (2) m=0, p≠0. Тогда мы заключаем, что x−x1=0.
Выше мы отметили, что прямая L проходит через точку M1(x1, y1). В этом можно убедится, подставив x=x1, y=y1 в уравнение (1).
Запишем каноническое уравнение прямой проходящей через две различные точки M1(x1, y1) и M2(x2, y2):
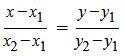 . . |
(3) |
Чтобы убедится, что точки M1(x1, y1) и M2(x2, y2) находятся на прямой L, поочередно подставим в уравнение (3) координаты точек M1 и M2. Получим тождества, следовательно эти точки принадлежат прямой L.
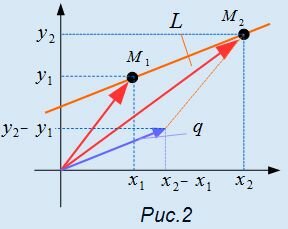 |
Сравним уравнения (1) и (3). Тогда можно записать q={m, p}={x2−x1, y2−y1}. На рисунке Рис.2 представлен вектор q, которая является разностью векторов, соответствующих точкам M2 и M1. Этот вектор является направляющим вектором прямой L. Следовательно, для определения направляющего вектора прямой, достаточно взять две точки на данной прямой и найти разность между соответсвующими координатами этих точек.
Таким образом, прямая на плоскости определяется точкой и направляющим вектором или двумя точками.
Онлайн калькулятор, для построения прямой через две точки находится тут.
Пример 1. Прямая проходит через точку M=(3,−1) и имеет направляющий вектор q={−3, 5}. Построить каноническое уравнение прямой.
Решение. Для построения канонического уравнения прямой, подставим координаты точки и направляющего вектора в уравнение (1):
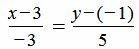 . . |
Ответ:
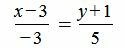 . . |
Пример 2. Прямая проходит через точку M=(2, 2) и имеет направляющий вектор q={0, 3}. Построить каноническое уравнение прямой.
Решение. Для построения канонического уравнения прямой, подставим координаты точки и направляющего вектора в уравнение (1):
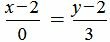 . . |
Ответ:
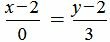 . . |
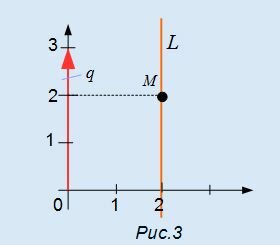
На рисунке Рис.3 изображена прямая L, точка M=(2, 2) и направляющий вектор q={0, 3}. Прямая проходит через точку M и параллельна направляющему вектору q.
 |
Пример 3. Прямая проходит через точки M1=(−7, 2) и M2=(−4, 4). Построить каноническое уравнение прямой. Воспользуемся формулой (3). Подставим координаты точек в уравнение (3):
 . . |
Упростим полученное уравнение:
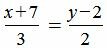 . . |
Ответ:
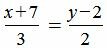 . . |
Для приведения канонического уравнения прямой на плоскости к параметрическому виду, обозначим каждую часть уравнения (1) переменным t:
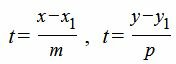 . . |
Выразим переменные x и y через t:
 , , |
(4) |
где t называется параметром, а уравнение (4) называется параметрическим уравнением прямой.
Для построения уравнения прямой, представленной параметрическом виде (4), достаточно задать параметру t любые значения и вычислить из уравнений (4) соответствующие координаты x и y некоторых точек. Затем провести через эти точки прямую.
Обратное преобразование смотрите здесь.
Пример 4. Каноническое уравнение прямой задана следующим уравнением:
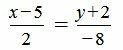 . . |
(5) |
Найти параметрическое уравнение прямой.
Решение. Обозначим через t левую и правую части уравнения (5):
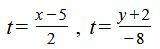 . . |
Выразим переменные x и y через t:
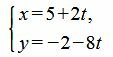 . . |
Ответ:
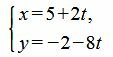 . . |
Пусть прямая на плоскости задана каноническим уравнением прямой (1). Преобразовав (1) получим:
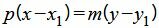 , , |
 . . |
(6) |
Сделаем следующие обозначения:
| A=p, B=−m, C=−px1+my1. |
Тогда уравнение (6) можно записать в следующем виде:
| Ax+By+C=0, |
где n={A,B} − называется нормальным вектором прямой.
Нетрудно заметить, что нормальный и направляющий векторы прямой перепендикулярны, т.е. скалярное произведение этих векторов равно нулю:
| (n,q)=({A,B},{m,p}) =({p,−m},{m,p})=pm−mp=0. |
Обратное преобразование смотрите здесь.
Пример 5. Каноническое уравнение прямой задана следующим уравнением:
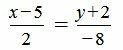 . . |
(7) |
Записать общее уравнение прямой.
Решение. Сделаем преобразования уравнения (7):
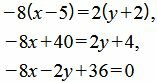 . . |
Ответ:
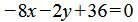 . . |