

С помощю этого онлайн калькулятора можно найти уравнение плоскости, проходящей через заданную точку и параллельной данной плоскости. Дается подробное решение с пояснениями. Для нахождения уравнения плоскости, введите координаты точки и коэффициенты уравнения плоскости в ячейки и нажимайте на кнопку "Решить".
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Пусть задана точка M0(x0, y0, z0) и уравнение плоскости
| Ax+By+Cz+D=0 | (1) |
Наша задача найти уравнение плоскости, проходящей через точку M0 и параллельной плоскости (1)(Рис.1).
 |
Все параллельные плоскости имеют коллинеарные нормальные векторы. Поэтому для построения параллельной к (1) плоскости, проходящей через точку M0(x0, y0, z0) нужно взять в качестве нормального вектора искомой плоскости, нормальный вектор n=(A, B, C) плоскости (1). Далее нужно найти такое значение D, при котором точка M0(x0, y0, z0) удовлетворяла уравнению плоскости (1):
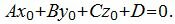 |
(2) |
Решим (2) относительно D:
| D=−(Ax0+By0+Cz0) | (3) |
Подставляя значение D из (3) в (1), получим:
| Ax+By+Cz−(Ax0+By0+Cz0)=0 | (4) |
Уравнение (4) можно представить также в следующем виде:
| A(x−x0)+B(y−y0)+C(z−z0)=0 | (5) |
Уравнение (5) является уравнением плоскости, проходящей через точку M0(x0, y0, z0) и параллельной плоскости (1).
Пример 1.
Найти уравнение плоскости, проходящей через точку M0(1, −6, 2) и параллельной плоскости :
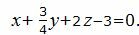 |
(6) |
Решение.
Запишем коэффициенты нормального вектора плоскости (6):
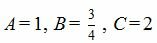 |
(7) |
Подставляя координаты точки M0 и координаты нормального вектора в (3), получим:
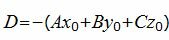 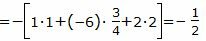 |
(8) |
Подставляя значения A, B, C, D в уравнение плоскости (1), получим:
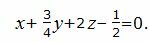 |
Уравнение плоскости можно представить в более упрощенном виде, умножив на 4:
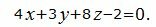 |
Ответ.
Уравнение плоскости, проходящей через точку M0(1, −6, 2) и параллельной плоскости (6) имеет следующий вид:
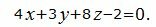 |