С помощю этого онлайн калькулятора можно найти угол между плоскостями. Дается подробное решение с пояснениями. Для вычисления угла между плоскостями, введите элементы уравнения плоскостей в ячейки и нажимайте на кнопку "Решить".
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Пусть заданы две плоскости α и β общими уравнениями
| A1x+B1y+C1z+D1=0, | (1) |
| A2x+B2y+C2z+D2=0 | (2) |
Угол между этими плоскостями сводится к определению угла φ между нормальными векторами n1=(A1, B1, C1) и n2=(A2, B2, C2) этих плоскостей.
Из определения скалярного произведения, имеем
 . |
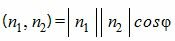(3) |
Тогда из (3) можно найти косинус угла между нормальными векторами n1 и n2:
 . |
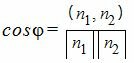(4) |
Учитывая, что (n1, n2)=A1A2+B1B2+C1C2 и длины векторов |n1|=
и |n2|=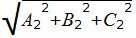
выражение (4) можно записать так:
 . |
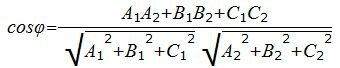(5) |
Таким образом косинус угла между нормальными векторами и, следовательно, косинус угла между плоскостями α и β определяется формулой (5). Далее можно найти угол φ с помощью функции arccos.
Отметим, что пересекающиеся плоскости образую два угла. Другой угол можно найти так: φ'=180−φ.
Пример 1. Найти угол между плоскостями
 |
(6) |
и
 |
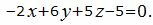(7) |
Решение.
Нормальный вектор плоскости (6) равен n1=(A1, B1, C1)=(1, 2, -6), нормальный вектор плоскости (7) равен n2=(A2, B2, C2)=(-2, 6, 5).
Подставим значения A1, B1, C1, A2, B2, C2 в (5):
 |
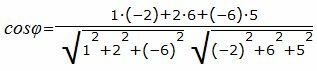(8) |
Упростим и решим:
 |
Найдем угол φ:
 |
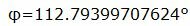Данный угол больше 90°. Найдем минимальный угол между плоскостями. Для этого вычтем этот угол из 180:
 |
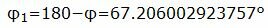Пример 2. Найти угол между плоскостями
 |
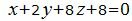(9) |
и
 |
(10) |
Решение.
Нормальный вектор плоскости (9) равен n1=(A1, B1, C1)=(1, 2, 8), нормальный вектор плоскости (10) равен n2=(A2, B2, C2)=(2, 4, 16).
Подставим значения A1, B1, C1, A2, B2, C2 в (5):
 |
Упростим и решим:
 |
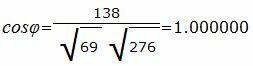Найдем угол φ:
 . |
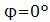Угол между этими плоскостями равен нулю. Следовательно эти плоскости параллельны.