

С помощю этого онлайн калькулятора можно найти точку пересечения прямых на плоскости. Дается подробное решение с пояснениями. Для нахождения координат точки пересечения прямых задайте вид уравнения прямых ("канонический", "параметрический" или "общий"), введите коэффициенты уравнений прямых в ячейки и нажимайте на кнопку "Решить". Теоретическую часть и численные примеры смотрите ниже.
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Пусть задана декартова прямоугольная система координат Oxy и пусть в этой системе координат заданы прямые L1 и L2:
| L1: A1x+B1y+C1=0, | (1) |
| L2: A2x+B2y+C2=0 | (2) |
где n1={A1, B1} и n2={A2, B2} − нормальные векторы прямых L1 и L2, соответственно.
Для нахождения точки пересечения прямых (1) и (2) нужно решить систему линейных уравнений (1) и (2) относительно переменных x,y. Для этого запишем систему (1),(2) в матричном виде:
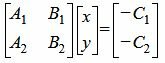 |
(3) |
Построим расширенную матрицу:
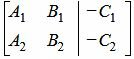 |
(4) |
Приведем (4) к верхнему диагональному виду. Пусть A1≠0 . Тогда сложим строку 2 со строкой 1, умноженной на −A2/A1:
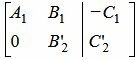 |
(5) |
где
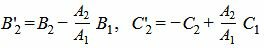 |
Если B'2=0 и С'2=0, то система линейных уравнений имеет множество решений. Следовательно прямые L1 и L2 совпадают. Если B'2=0 и С'2≠0, то система несовместна и, следовательно прямые параллельны и не имеют общей точки. Если же B'2≠0, то система линейных уравнений имеет единственное решение. Из второго уравнения находим y: y=С'2/B'2 и подставляя полученное значение в первое уравнение находим x: x=(−С1−B1y)/A1. Получили точку пересечения прямых L1 и L2: M(x, y).
Подробнее о решении систем линейных уравнений посмотрите на странице метод Гаусса онлайн.
Пусть задана декартова прямоугольная система координат Oxy и пусть в этой системе координат заданы прямые L1 и L2:
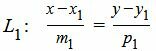 |
(6) |
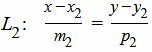 |
(7) |
где M1(x1, y1) и M2(x2, y2) − точки, лежащие на прямых L1 и L2, соответственно, а q1={m1, p1} и q2={m2, p2} − направляющие векторы прямых L1 и L2, соответственно.
Приведем уравнение L1 к общему виду. Сделаем перекрестное умножение в уравнении (6):
| p1(x−x1)=m1(y−y1) |
Откроем скобки и сделаем преобразования:
| p1x−m1y−p1x1+m1y1=0 |
Обозначив A1=p1, B1=−m1, C1=−p1x1+m1y1, получим общее уравнение прямой (6):
| A1x+B1y+C1=0 | (8) |
Аналогичным методом получим общее уравнение прямой (7):
| A2x+B2y+C2=0 | (9) |
Терерь можно найти точку пересечения прямых L1 и L2 методом, описанным в параграфе 1.
Пусть задана декартова прямоугольная система координат Oxy и пусть в этой системе координат заданы прямые L1 и L2 в параметрическом виде:
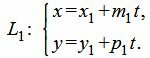 |
(10) |
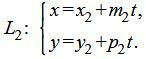 |
(11) |
где M1(x1, y1) и M2(x2, y2) − точки, лежащие на прямых L1 и L2, соответственно, а q1={m1, p1} и q2={m2, p2} − направляющие векторы прямых L1 и L2, соответственно.
Приведем уравнение прямой L1 к каноническому виду. Для этого из уравнений (10) найдем параметр t:
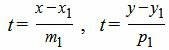 |
(12) |
Из уравнений (12) следует:
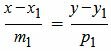 |
Аналогичным образом можно найти каноническое уравнение прямой L2:
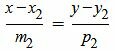 |
Как найти точку пересечения прямых, заданных в каноническом виде описано выше.
Пусть задана декартова прямоугольная система координат Oxy и пусть в этой системе координат заданы прямые L1 и L2:
| L1: A1x+B1y+C1=0, | (13) |
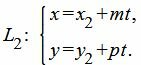 |
(14) |
где n={A1, B1} нормальный вектор прямой L1, q={m, p} − направляющий вектор прямой L2 .
Найдем точку пересечения прямых L1 и L2. Для этого подставим x=x2+mt, y=y2+pt в (13):
| A1(x2+mt)+B1(y2+pt)+C1=0, | (15) |
Найдем t:
| A1x2+A1mt+B1y2+B1pt+C1=0, |
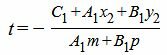 |
(16) |
Если числитель и знаменатель в (16) одновременно равны нулю, то любое значение t удовлетворяет уравнению (15), следовательно прямые L1 и L2 совпадают. Если знаменатель равен нулю а числитель отличен от нуля, то прямые L1 и L2 не пересекаются, т.е. они параллельны.
Пусть знаменатель не равен нулю. Подставляя полученное значение t в (14), получим координаты точки пересечения прямых L1 и L2.
Пример 1. Найти точку пересечения прямых L1 и L2:
| L1: 2x+y+4=0, | (17) |
| L2: x−3y+2=0. | (18) |
Для нахождения точки пересечения прямых L1 и L2 нужно решить систему линейных уравнений (17) и (18). Представим уравнения в матричном виде:
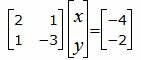 |
(19) |
Решим систему линейных уравнений отностительно x, y. Для этого воспользуемся методом Гаусса. Получим:
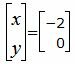 |
Ответ. Точка пересечения прямых L1 и L2 имеет следующие координаты:
| M (−2, 0). |
Пример 2. Найти точку пересечения прямых L1 и L2:
| L1: 2x+3y+4=0, | (20) |
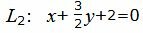 |
(21) |
Для нахождения точки пересечения прямых L1 и L2 нужно решить систему линейных уравнений (20) и (21). Представим уравнения в матричном виде:
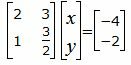 |
(22) |
Для решения (22) воспользуемся методом Гаусса. Получим:
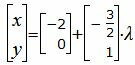 |
где λ− произвольное действительное число.
Имеем больше одного решения. Это означает, что прямые L1 и L2 совпадают.
Ответ. Прямые L1 и L2 совпадают.
Пример 3. Найти точку пересечения прямых L1 и L2:
| L1: −5x+y+9=0, | (23) |
| L2: −10x+2y−3=0, | (24) |
Для нахождения точки пересечения прямых L1 и L2 нужно решить систему линейных уравнений (23) и (24). Представим уравнения в матричном виде:
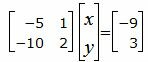 |
(25) |
Применив метод Гаусса получим, что система (25) несовместна. Следовательно эти прямые не пересекаются, т.е. они параллельны.
Ответ. Прямые L1 и L2 не имеют общую точку, т.е. они параллельны.
Пример 4. Найти точку пересечения прямых L1 и L2:
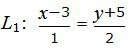 |
(26) |
| L2: x+2y−9=0, | (27) |
Приведем, сначала, уравнение прямой (26) к общему виду:
| 2(x−3)=y+5 |
| 2x−y−11=0 | (28) |
Для нахождения точки пересечения прямых L1 и L2 нужно решить систему линейных уравнений (28) и (27). Представим уравнения в матричном виде:
 |
(29) |
Решим систему линейных уравнений отностительно x, y:
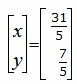 |
Ответ. Точка пересечения прямых L1 и L2 имеет следующие координаты:
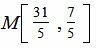 . . |