

С помощю этого онлайн калькулятора можно найти расстояние между плоскостями. Дается подробное решение с пояснениями. Для нахождения расстояния между плоскостями, введите элементы уравнения плоскости в ячейки и нажимайте на кнопку "Решить".
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Заметим, сначала, что расстояние между плоскостями определена, если плоскости параллельны или, что то же самое, нормальные векторы этих плоскостей коллинеарны. Вычисление расстояния между двумя плоскостями можно свести к вычислению расстояния от точки первой плоскости до второй плоскости. Вычисление расстояния от точки до плоскости (онлайн калькулятор, теория, примеры) посмотрите на странице Расстояние от точки до плоскости онлайн.
Алгоритм вычисления расстояния между плоскостями содержит следующие шаги:
 |
Выведем формулу вычисления расстояния между плоскостями.
Запишем уравнения двух плоскостей:
| A1x+B1y+C1z+D1=0 | (1) |
| A2x+B2y+C2z+D2=0 | (2) |
1. Проверяем коллинеарность нормальных векторов n1=(A1, B1, C1) и n2=(A2, B2, C2).
Очевидно, что нормальные векторы n1 и n2 не могут быть нулевыми векторами.Если из пары коэффициентов (A1,A2),(B1,B2), (C1,C2) один нулевой а другой − нет, то нормальные векторы n1 и n2 неколлинеарны. Т.е. задача неразрешима.
Пусть A1≠0, A2≠0. Уравнение плоскости (2) не изменится, если умножим на A1/A2:
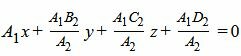 |
(2') |
Нормальный вектор уравнения (2') имеет следующий вид:
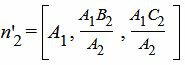 |
Для коллинеарности векторов n1 и n'2(или n1 и n2) необходимо и достаточно выполнение следующих равенств:
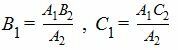 |
(3) |
или
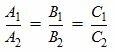 |
(3') |
Если удовлетворяется условие (3) (или (3')), то векторы n1 и n'2(или n1 и n2) коллинеарны, т.е. плоскости (1) и (2') (или (1) и (2) ) параллельны. Тогда уравнение плоскости (2') можно представить так:
| A1x+B1y+C1z+D'2=0 | (2'') |
где
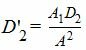 |
2. Найдем некоторую точку на плоскости (1).
Легко убедится, что точка
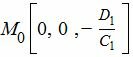 |
(4) |
принадлежит плоскости (1):
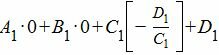 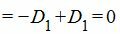 |
3. Расстояние от точки M0(x0, y0, z0) до плоскости (2'') вычисляется с помощью выражения (подробнее смотрите на странице расстояние от точки до плоскости):
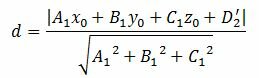 |
(5) |
Подставляя координаты точки M0 из (4) в (5), получим формулу вычисления расстояния между плоскостями (1) и (2'') (или (1) и (2)):
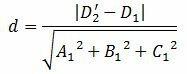 |
(6) |
где
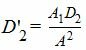 |
Пример 1. Найти расстояние между плоскостями
 |
(7) |
и
 |
(8) |
Решение.
Проверим, являются ли эти плоскости параллельными. Для этого умножим второе уравнение на 1/3.
 |
(8') |
Общее уравнение плоскости имеет вид:
| Ax+By+Cz+D=0 |
где n=(A,B,C)− называется нормальным вектором плоскости.
Нормальный вектор плоскости (7) равен n1=(1, 2, −4), нормальный вектор плоскости (8') равен n2=(1, 2, −4). n1=n2. Следовательно эти плоскости параллельны.
Найдем расстояние между плоскостями (7) и (8'), используя следующую формулу:
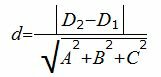 |
(9) |
Подставим значения A, B, C, D1, D2 в (9):
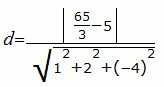 |
Упростим и решим:
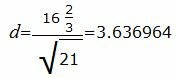 |
Ответ. Расстояние между плоскостями равен:
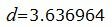 |
Пример 2. Найти расстояние между плоскостями
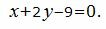 |
(10) |
и
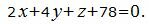 |
(11) |
Решение.
Эти плоскости не параллельны, так как коэффициент переменного z уравнения (10) нулевой а коэффициент переменного z уравнения (11)−нет. Невозможно найти расстояние между непараллельными плоскостями.
Пример 3. Найти расстояние между плоскостями
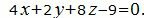 |
(12) |
и
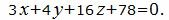 |
(13) |
Решение.
Проверим, являются ли эти плоскости параллельными. Для этого умножим второе уравнение на 4/3.
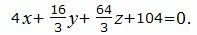 |
(13') |
Нормальный вектор плоскости (12) равен n1=(4, 2, 8), нормальный вектор плоскости (13') равен n2=(4, 16/3, 64/3). n1≠n2. Нормальные векторы этих плоскостей неколлинеарны. Тогда эти плоскости не параллельны и, следовательно, задача неразрешима.