В данной статье мы рассмотрим общее уравнение прямой на плоскости. Приведем примеры построения общего уравнения прямой, если известны две точки этой прямой или если известна одна точка и нормальный вектор этой прямой. Представим методы преобразования уравнения в общем виде в канонический и параметрический виды.
Пусть задана произвольная декартова прямоугольная система координат Oxy. Рассмотрим уравнение первой степени или линейное уравнение:
| Ax+By+C=0, | (1) |
где A, B, C − некоторые постоянные, причем хотя бы один из элементов A и B отлично от нуля.
Мы покажем, что линейное уравнение на плоскости определяет прямую. Докажем следующую теорему.
Теорема 1. В произвольной декартовой прямоугольной системе координат на плоскости каждая прямая линия может быть задана линейным уравнением. Обратно, каждое линейное уравнение (1) в произвольной декартовой прямоугольной системе координат на плоскости определяет прямую линию.
Доказательство. Достаточно доказать, что прямая L определяется линейным уравнением при какой нибудь одной декартовой прямоугольной системе координат, поскольку тогда она будет определяться линейным уравнением и при любом выборе декартовой прямоугольной системы координат.
Пусть на плоскости задана прямая L. Выберем систему координат так, чтобы ось Ox совпадал с прямой L, а ось Oy был перпендикулярной к ней. Тогда уравнение прямой L примет следующий вид:
| y=0. | (2) |
Все точки на прямой L будут удовлетворять линейному уравнению (2), а все точки вне этой прямой, не будут удовлетворять уравнению (2). Первая часть теоремы доказана.
Пусть задана декартова прямоугольная система координат и пусть задана линейное уравнение (1), где хотя бы один из элементов A и B отличен от нуля. Найдем геометрическое место точек, координаты которых удовлетворяют уравнению (1). Так как хотя бы один из коэффициентов A и B отличен от нуля, то уравнение (1) имеет хотя бы одно решение M(x0,y0). (Например, при A≠0, точка M0(−C/A, 0) принадлежит данному геометрическому месту точек). Подставляя эти координаты в (1) получим тождество
| Ax0+By0+C=0. | (3) |
Вычтем из (1) тождество (3):
| A(x−x0)+B(y−y0)=0. | (4) |
Очевидно, что уравнение (4) эквивалентно уравнению (1). Поэтому достаточно доказать, что (4) определяет некоторую прямую .
Поскольку мы рассматриваем декартову прямоугольную систему координат, то из равенства (4) следует, что вектор с компонентами {x−x0, y−y0} ортогонален вектору n с координатами {A,B}.
Рассмотрим некоторую прямую L, проходящую через точку M0(x0, y0) и перпендикулярной вектору n (Рис.1). Пусть точка M(x,y) принадлежит прямой L. Тогда вектор 
с координатами x−x0, y−y0 перпендикулярен n и уравнение (4) удовлетворено (скалярное произведение векторов n и равно нулю). Обратно, если точка M(x,y) не лежит на прямой L, то вектор с координатами x−x0, y−y0 не ортогонален вектору n и уравнение (4) не удовлетворено. Теорема доказана.
 |
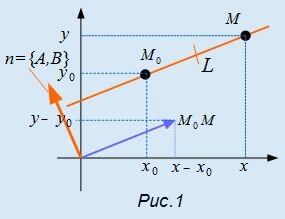Вектор n={A,B} называется нормальным вектором прямой L.
Замечание 1. Если два общих уравнения прямой
| A1x+B1y+C1=0 | (5) |
и
| A2x+B2y+C2=0 | (6) |
определяют одну и ту же прямую, то найдется такое число λ, что выпонены равенства
| A2=A1λ, B2=B1λ, C2=C1λ. | (7) |
Доказательство. Так как прямые (5) и (6) определяют одну и ту же прямую, то нормальные векторы n1={A1,B1} и n2={A2,B2} коллинеарны. Так как векторы n1≠0, n2≠0, то существует такое число λ, что n2=n1λ. Отсюда имеем: A2=A1λ, B2=B1λ. Докажем, что C2=C1λ. Очевидно, что совпадающие прямые имеют общую точку M0(x0, y0). Умножая уравнение (5) на λ и вычитая из него уравнение (6) получим:
| (A1λ−A2)x0+(B1λ−B2)x0+(C1λ−C2)=0. | (8) |
Так как выполнены первые два равенства из выражений (7), то C1λ−C2=0. Т.е. C2=C1λ. Замечание доказано.
Заметим, что уравнение (4) определяет уравнение прямой, проходящей через точку M0(x0, y0) и имеющий нормальный вектор n={A,B}. Поэтому, если известен нормальный вектор прямой и точка, принадлежащая этой прямой, то можно построить общее уравнение прямой с помощью уравнения (4).
Пример 1. Прямая проходит через точку M=(4,−1) и имеет нормальный вектор n={3, 5}. Построить общее уравнение прямой.
Решение. Имеем: x0=4, y0=−1, A=3, B=5. Для построения общего уравнения прямой, подставим эти значения в уравнение (4):
| 3(x−4)+5(y−(−1))=0 |
Упростив получим общее уравнение прямой:
| 3x+5y−7=0. |
Ответ:
| 3x+5y−7=0. |
Пример 2. Прямая проходит через точки M1=(−5, 2) и M2=(−2, 3). Построить общее уравнение прямой.
Решение. Вычислим вектор 
:
 |
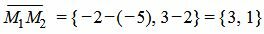Вектор параллелен прямой L и, следовательно, перпердикулярен нормальному вектору прямой L. Построим нормальный вектор прямой L, учитывая, что скалярное произведение векторов n и равно нулю. Можем записать, например, n={1,−3}.
Для построения общего уравнения прямой воспользуемся формулой (4). Подставим в (4) координаты точки M1 (можем взять также координаты точки M2) и нормального вектора n:
| 1(x−(−5))−3(y−2)=0. |
Упростим полученное уравнение:
| x−3y+6=0. | (9) |
Подставляя координаты точек M1 и M2 в (9) можем убедится, что прямая заданная уравнением (9) проходит через эти точки.
Ответ:
| x−3y+6=0. |
Нам нужно привести уравнение (1) к каноническому виду. Для этого найдем некоторую точку M0(x0,y0) на этой прямой. Тогда имеем:
| Ax0+By0+C=0 | (10) |
Вычтем (10) из (1):
| A(x−x0)+B(y−y0)=0 | (11) |
Вторую слагаемую уравнения (11) переместим на право и разделим обе части уравнения на −AB:
 |
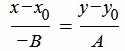(12) |
Мы получили каноническое уравнение прямой. Вектор q={−B, A} является направляющим вектором прямой (12).
Обратное преобразование смотрите здесь.
Пример 3. Прямая на плоскости представлена следующим общим уравнением:
| 2x−5y+1=0. | (13) |
Привести данное уравнение прямой к каноническому виду.
Решение: Найдем некоторую точку на прямой (13). Для этого подставим в (13) y=1 и найдем x. Получим x=2. Запишем уравнение прямой пользуясь формулой (11):
| 2(x−2)−5(y−1)=0. |
Переместим на право вторую слагаемую и разделим обе части уравнения на 2·5:
 |
Ответ.
|
В предыдущем параграфе мы привели общее уравнение прямой (1) к каноническому виду (12). Из канонического уравнения легко получить параметрическое уравнение прямой. для этого левый и правый части уравнения (12) обозначим через параметр t. Тогда получим:
 |
Выразив x и y через параметр t, получим параметрическое уравнение прямой:
 |
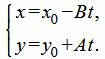Обратное преобразование смотрите здесь.
Пример 4. Прямая на плоскости представлена следующим общим уравнением:
| 5x−2y+7=0 | (14) |
Привести данное уравнение прямой к параметрическому виду.
Решение: Найдем некоторую точку на прямой (13). Для этого подставим в (14) x=3 и найдем y. Получим y=11. Запишем уравнение прямой пользуясь формулой (11):
| 5(x−3)−2(y−11)=0 |
Переместим на право вторую слагаемую и разделим обе части уравнения на 5·2:
 |
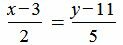Обозначим обе части уравнения через параметр t:
 |
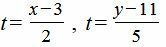Выразим x и y через параметр t:
 |
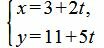Ответ. Параметрическое уравнение прямой имеет следующий вид:
|
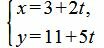