В данной статье мы рассмотрим понятие пучка прямых. Представим уравнение пучка прямых. Приведем примеры нахождения уравнения пучка прямых, проходящих через данную точку.
Пучком прямых называется множество прямых, проходящих через данную точку P. P называется центром пучка прямых. Две разные прямые в пучке прямых определяют центр пучка прямых.
 |
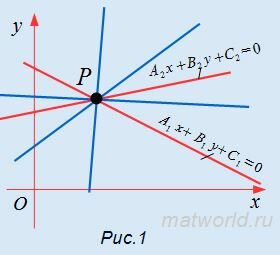Найдем уравнение пучка прямых, центром которого служит точка пересечения двух прямых (Рис.1):
| A1x+B1y+C1=0 | (1) |
и
| A2x+B2y+C2=0. | (2) |
Докажем следующую теорему.
Теорема 1. Пусть (1) и (2) уравнения двух прямых, пересекающихся в точке P, а λ1 и λ2 некоторые числа, которые одновременно не равны нулю. Тогда
| λ1(A1x+B1y+C1) +λ2(A2x+B2y+C2)=0. | (3) |
является уравнением прямой, проходящей через точку P. Обратно, любая прямая, проходящая через точку P определяется уравнением (3), при некотороых числах λ1 и λ2.
Доказательство. Во первых покажем, что уравнение (3) является линейным уравнением (уравнением первого порядка), т.е. уравнением, при котором коэффициент при x или y не равен нулю.
Группируем коэффициенты при x и y:
| (λ1A1+λ2A2)x+(λ1B1+λ2B2)y+(λ1C1+λ2C2)=0 | (4) |
Пусть
| λ1A1+λ2A2=0, λ1B1+λ2B2=0. | (5) |
Тогда, например при λ1≠0 (по условию теоремы хотя бы один из чисел λ1 и λ2 не равен нулю), получим:
 | (6) |
т.е.
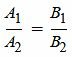 . | (7) |
Полученное равенство является условием параллельности прямых, определяемых уравнениями (1) и (2), что противоречит условию теоремы (эти прямые пересекаются и не совпадают). Таким образом хотя бы один из равенств (5) не выполняется, т.е. хотя бы один коэффициент при x и y в уравнении (4) не равен нулю. Отсюда следует, что уравнение (4) является линейным уравнением (уравнением первой степени) и является уравнением некоторой прямой. По условию теоремы, эта прямая проходит через точку P(x0, y0), которая является пересечением прямых (1) и (2), т.е. выполняются равенства:
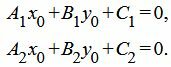 | (8) |
Из уравнениий (8) следует, что при любых λ1 и λ2:
| λ1(A1x0+B1y0+C1)+λ2(A2x0+B2y0+C2)=0, |
т.е. уравнение (3) проходит через точку P.
Докажем вторую часть теоремы. Покажем, что любая прямая, проходящая через точку P определяется уравнением (3) при некоторых значениях λ1 и λ2.
Возьмем некоторую прямую проходящую через точки P и M'(x', y'). Покажем, что данная прямая определяется уравнением (3) при некоторых значениях λ1 и λ2, не равных одновременно нулю.
В первой части доказательства теоремы мы показали, что прямая, проходящая через точку P определяется уравнением (3). Теперь, если эта прямая проходит через еще одну точку M'(x', y'), то координаты этой точки должны удовлетворять уравнению (3):
| λ1(A1x'0+B1y'0+C1)+λ2(A2x'0+B2y'0+C2)=0, | (9) |
Заметим, что выражения в скобках не могут быть равным нулю одновременно, т.к. это означало бы, что оба уравнения проходят через точки P и M'(x', y') и, следовательно, совпадают. Пусть, например, λ1(A1x'0+B1y'0+C1)≠0. Тогда задав λ2 произвольное число, отличное от нуля, решим (9) относительно λ1:
 |
Таким образом, при указанных коэффициентов λ1 и λ2, прямая (3) проходит через точки P и M'(x', y'). Если же λ1(A2x'0+B2y'0+C2)≠0, то аналогичным образом вычисляются коэффициенты λ1 и λ2.
Теорема доказана.
Пример 1. Пучок прямых задан уравнениями:
| 2x+3y−1=0 | (10) |
и
| x−4y+2=0. | (11) |
Найти уравнение прямой из пучка прямых, проходящий через точку M(−3, 1).
Решение. Уравнение пучка прямых, заданных прямыми (10) и (11) имеет следующий вид:
| λ1(2x+3y−1)+λ2(x−4y+2)=0. | (12) |
Подставим координаты точки M в уравннение (12):
| λ1(2·(−3)+3·1−1)+λ2(−3−4·1+2)=0. | (13) |
Упростим (13):
| λ1(−4))+λ2(−5)=0. |
Задав, например, λ2=4, получим λ1=−5.
Положим значения λ1 и λ2 в (12):
| −5(2x+3y−1)+4(x−4y+2)=0. | (14) |
Упростив уравнение (14), получим уравнение из пучка прямых проходящих через точку M(−3, 1):
| −6x−31y+13=0. |
Ответ:
| −6x−31y+13=0. |
Пример 2. Построить уравнение пучка прямых с центром M(4,1):
Решение. Возьмем две различные точки, не совпадающие с точкой M: M1(2,1), M2(−1,3). Построим уравнение, проходящие через точки M и M1. Нормальный вектор n1 этой прямой должен быть ортогональным вектору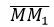 
, равному разностьям координат точек M и M1: 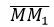={2−4, 1−1}={−2,0}. Т.е. можно взять n1={0,1}. Тогда уравнение прямой с нормальным вектором n1, проходяще через точку M имеет следующий вид:
| 0(x−4)+1(y−1)=0 |
или
| y−1=0. | (15) |
Построим уравнение проходящее через точки M и M2.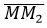 
={−1−4, 3−1}={−5,2}. Возмем в качестве нормального вектора второго уравнения n2={2, 5}. Тогда второе уравнение имеет слеждующий вид:
| 2(x−4)+5(y−1)=0 |
или
| 2x+5y−13=0. | (16) |
Из уравнений (15) и (16) можно записать уравнение пучка прямых с центром M(4,1):
| λ1(y−1)+λ2(2x+5y−13)=0. |
Ответ:
| λ1(y−1)+λ2(2x+5y−13)=0. |
Заметим, что взяв другие точки M1 и M2, мы получим уравнение того же пучка прямых, но с другими двумя прямыми.