С помощю этого онлайн калькулятора можно найти расстояние от точки до прямой. Дается подробное решение с пояснениями. Для вычисления расстояния от точки до прямой, задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), введите координаты точки и элементы уравнения в ячейки и нажимайте на кнопку "Решить".
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Рассмотрим эту задачу в двухмерном и трехмерном пространствах.
Пусть в двухмерном пространстве задана точка M0(x0, y0) и прямая L:
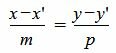 , , |
(1) |
где q=(m,p) направляющий вектор прямой L.
Найдем расстояние от точки M0 до прямой (1)(Рис.1).
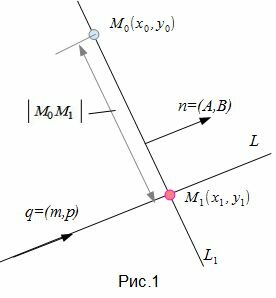 |
Алгоритм нахождения расстояния от точки M0 до прямой L содержит следующие шаги:
Уравнение прямой, проходящей через точку M0(x0, y0) имеет следующий вид:
| A(x−x0)+B(y−y0)=0 | (2) |
где n=(A,B) нормальный вектор прямой L1.
Как видно из рисунка Рис.1, для того, чтобы прямая L1 была перпендикулярна прямой L нужно , чтобы направляющий вектор q прямой L была коллинеарна нормальному вектору n прямой L1, поэтому в качестве нормального вектора прямой L1 достаточно взять направляющий вектор прямой L. Тогда уравнение прямой L1, представленной уравнением (2) можно записать так:
| m(x−x0)+p(y−y0)=0 | (3) |
Откроем скобки
| mx+py−mx0−py0=0 | (4) |
Для нахождения точки пересечения прямых L и L1, которая и будет проекцией точки M0 на прямую L, можно решить систему из двух уравнений (1) и (3) с двумя неизвестными x и y. Выражая неизвестную x из одного уравнения и подставляя в другое уравнение получим координаты точки M1(x1, y1).
Найдем точку пересечения прямых L и L1 другим методом.
Выведем параметрическое уравнение прямой (1):
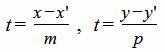 |
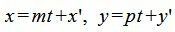 |
(5) |
Подставим значения x и y в (4):
| m(mt+x')+p(pt+y')−mx0−py0=0 |
| m2t+mx'+p2t+py'−mx0−py0=0 |
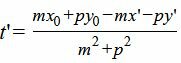 |
(6) |
Мы нашли такое значение t=t', при котором координаты x и y точки на прямой L удовлетворяют уравнению прямой L1(4). Следовательно, подставляя значение t' в (5) получим координаты проекции точки M0 на прямую L:
| M1(x1, y1), |
где x1=mt'+x', y1=pt'+y'.
Далее находим расстояние между точками M0 и M1 используя формулу:
 . . |
(7) |
Пример 1. Найти расстояние от точки M0(−6, 2) до прямой
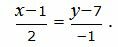 |
(8) |
Решение.
Направляющий вектор прямой (8) имеет вид:
| q=(2, −1) |
Т.е. m=2, p=−1. Из уравнения прямой (8) видно, что она проходит через точку M' (x', y')=(1, 7)(в этом легко убедится − подставляя эти значения в (8) получим тождество 0=0), т.е. x'=1, y'=7. Подставим значения m, p, x0, y0, x', y' в (6):
 |
 |
 , , |
Подставляя значение t в (5), получим:
 |
Вычислим расстояние между точками M0(-6, 2) и M1
 |
Упростим и решим:
  |
Ответ:
Расстояние от точки M0(-6, 2) до прямой (8) :
 |
Пусть в трехмерном пространстве задана точка M0(x0, y0, z0) и прямая L:
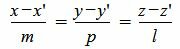 , , |
(9) |
где q=(m, p, l) направляющий вектор прямой L.
Найдем расстояние от точки M0 до прямой (9)(Рис.2).
 |
Алгоритм нахождения расстояния от точки до прямой L содержит следующие шаги:
Уравнение плоскости, проходящей через точку M0(x0, y0, z0) имеет следующий вид:
| A(x−x0)+B(y−y0)+C(z−z0)=0 | (10) |
где n=(A,B,C) нормальный вектор плоскости α.
Как видно из рисунка Рис.2, для того, чтобы плоскость α была перпендикулярна прямой L нужно , чтобы направляющий вектор q прямой L была коллинеарна нормальному вектору n плоскости α, поэтому в качестве нормального вектора плоскости α достаточно взять направляющий вектор прямой L. Тогда уравнение плоскости α, представленной уравнением (10) можно записать так:
| m(x−x0)+p(y−y0)+l(z−z0)=0 |
Откроем скобки
| mx+py+lz−mx0−py0−lz0=0 | (11) |
Для нахождения точки пересечения плоскости α и прямой L, которая и будет проекцией точки M0 на прямую L, выведем параметрическое уравнение прямой (9):
 |
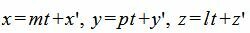 |
(12) |
Подставим значения x и y в (11):
| m(mt+x')+p(pt+y')+l(lt+z')−mx0−py0−lz0=0 |
| m2t+mx'+p2t+py'+l2t+ly'−mx0−py0−lz0=0 |
 |
(13) |
Мы нашли такое значение t=t', при котором координаты x,y и z точки на прямой L удовлетворяют уравнению плоскости (11). Следовательно, подставляя значение t' в (12) получим координаты проекции точки M0 на прямую L:
| M1(x1, y1, , z1), |
где x1=mt'+x', y1=pt'+y', z1=lt'+z'.
Далее вычисляем расстояние между точками M0 и M1 используя формулу
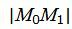 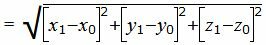 , , |
(14) |
которое является расстоянием между точкой M0 и прямой (9).
Пример 2. Найти расстояние от точки M0(1, 2, 1) до прямой
 |
(15) |
Решение.
Направляющий вектор прямой (15) имеет вид:
| q=(2, 4, 6) |
Т.е. m=2, p=4, l=−6. Из уравнения прямой (15) видно, что она проходит через точку M' (x', y', z')=(4, 3, 1)(в этом легко убедится − подставляя эти значения в (15) получим тождество 0=0=0), т.е. x'=4, y'=3, z'=1. Подставим значения m, p, l x0, y0, z0 x', y', z' в (13):
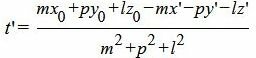 |
 |
 |
Подставляя значение t=t' в (12), получим координаты точки M1:
 , , |
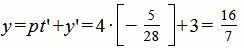 , , |
 . . |
Далее, используя формулу (14) вычисляем расстояние от точки M0 до прямой (15):
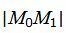 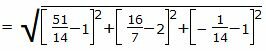 . . |
Упростим и решим:
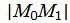   . . |
Ответ:
Расстояние от точки M0(1, 2, 1) до прямой (15) :
 |