

С помощю этого онлайн калькулятора можно построить уравнение прямой, проходящей через две точки. Дается подробное решение с пояснениями. Для построения уравнения прямой задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), введите координаты точек в ячейки и нажимайте на кнопку "Решить".
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Пример 1. Построить прямую, проходящую через точки A(2, 1, 1), B(3, 1, -2).
Решение.
Уравнение прямой, проходящей через точки A(x1, y1, z1) и B(x2, y2, z2) имеет следующий вид:
 |
(1) |
Подставив координаты точек A и B в уравнение (1), получим:
 |
или
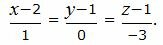 |
(Здесь 0 в знаменателе не означает деление на 0).
Составим параметрическое уравнение прямой:
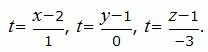 |
Выразим переменные x, y, z через параметр t :
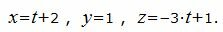 |
Ответ.
Каноническое уравнение прямой, проходящей через точки A(2, 1, 1), B(3, 1, -2) имеет следующий вид:
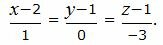 |
Параметрическое уравнение прямой, проходящей через точки A(2, 1, 1), B(3, 1, -2) имеет следующий вид:
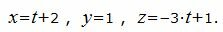 |
Пример 2. Построить прямую, проходящую через точки A(1, 1/5, 1) и B(−2, 1/2, −2).
Решение.
Уравнение прямой, проходящей через точки A(x1, y1, z1) и B(x2, y2, z2) имеет следующий вид:
 |
(2) |
Подставив координаты точек A и B в уравнение (2), получим:
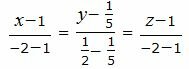 |
или
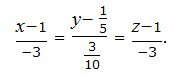 |
Составим параметрическое уравнение прямой:
 |
Выразим переменные x, y, z через параметр t :
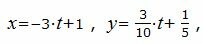 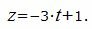 |
Ответ.
Каноническое уравнение прямой, проходящей через точки A(1, 1/5, 1) и B(−2, 1/2, −2) имеет следующий вид:
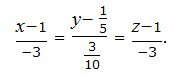 |
Параметрическое уравнение прямой, проходящей через точки A(1, 1/5, 1) и B(−2, 1/2, −2) имеет следующий вид:
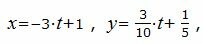 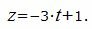 |