

С помощю этого онлайн калькулятора можно найти расстояние между точками по известным координатам этих точек. Дается решение с пояснениями. Для нахождения расстояния между точками задайте размерность (2-если задача рассматривается в двухмерном пространстве, 3- если задача рассматривается в трехмерном пространстве), введите координаты точек в ячейки и нажмите на кнопку "Решить". Теоретическую часть смотрите ниже.
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Пусть заданы на оси OX точки A с координатой xa и B с координатой xb (Рис.1). Найдем расстояние между точками A и B.
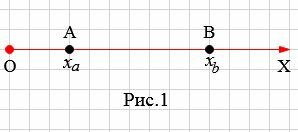 |
Расстояние между точками A и В равно:
| \( \small AB=OB-OA. \) | (1) |
Поскольку расстояние от O до В равна xb, а расстояние от O до A равна xa, получим:
| \( \small AB=x_b-x_a . \) | (2) |
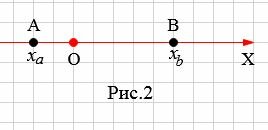 |
На рисунке 2 точки A и В находятся по разные стороны начала координат O. B этом случае рассояние между точками A и B равно:
| \( \small AB=OB+OA. \) | (3) |
Поскольку координата точки A отрицательна а координата точки B положительна, то (2) можно записать так:
| \( \small AB=x_b+|x_a|=x_b-x_a . \) | (4) |
На рисунке 3 точки A и В находятся c левой стороны начала координат O.
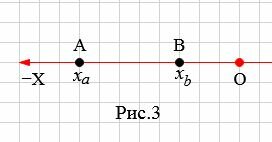 |
B этом случае рассояние между точками A и B равно:
| \( \small AB=OA-OB. \) | (5) |
Координаты точек A и B отрицательны. Тогда , то (5) можно записать так:
| \( \small AB=|x_a|-|x_b|=x_b-x_a . \) | (6) |
Из формул (2),(4),(6) следует, что независимо от расположения точек отностительно начала координат рассояние этих точек равна разности координат этих точек, причем от большего значения вычитается меньшее (так как расстояние не может быть отрицательным числом).
Формулы (2),(4),(6) можно записать и так:
| \( \small AB=|x_b-x_a|= |x_a-x_b| . \) | (7) |
Пример 1. на оси Ox заданы точки \( \small A(x_a)=A(-4) \) и \( \small B(x_b)=B(7) \) . Найти рассояние между этими точками.
Решение. Для нахождения расстояния между точками A и B воспользуемся формулой (7):
| \( \small AB=|x_b-x_a|= |7-(-4)|=11 . \) | (7) |
Ответ: 11.
Пусть на плоскости задана декартова прямоугольная система координат XOY и пусть на плоскости заданы точки A и B, где A имеет координаты (xa,ya), а B имеет координаты (xb,yb) (Рис.4).
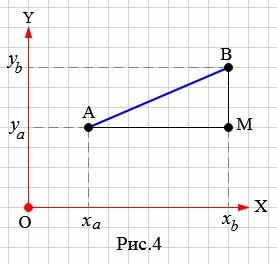 |
Учитывая результаты предыдующего параграфа, можем найти расстояние между точками A и M, а также расстояние между точками B и M:
| \( \small AM=x_b-x_a,\;\; BM=y_b-y_a. \) | (8) |
ABM является прямоугольным треугольником, где AB гипотенуза, а AM и BM катеты. Тогда, исходя из теоремы Пифагора, имеем:
| \( \small AB^2=AM^2+BM^2. \) |
Тогда, учитывая (8), получим:
| \( \small AB^2=AM^2+BM^2=(x_b-x_a)^2+(y_b-y_a)^2. \) |
Откуда:
| \( \small AB=\sqrt {(x_b-x_a)^2+(y_b-y_a)^2}. \) | (9) |
Пример 2. На плоскости, в декартовой прямоугольной системе координат XOY заданы точки \( \small A(x_a; \ y_a)=A(-6;3) \) и \( \small B(x_b, \ y_b)=B(11,-4). \) . Найти рассояние между этими точками.
Решение. Для нахождения расстояния между точками A и B воспользуемся формулой (9). Подставляя координаты точек A и B в формулу (9), получим:
 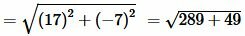 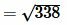 , , |
 . . |
Ответ: 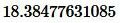 .
.
Рассмотрим в пространстве, в декартовой прямоугольной системе координат точки A и B, где A имеет координаты (xa,ya,za), а B имеет координаты (xb,yb,zb) (Рис.5).
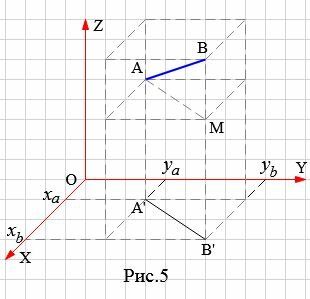 |
AB является диагональю параллелепипеда, грани которго параллельны координатным плоскостьям и проходят через точки A и B. Но AB является гипотенузой прямоугольного треугольника AMB, а AM и BM являются катетами этого прямоугольного треугольника. Тогда, по теореме Пифагора, имеем:
| \( \small AB^2=AM^2+BM^2. \) | (10) |
Учитывая, что BM равно разности третьих координат точек B и A, получим:
| \( \small BM=z_b-z_a. \) |
Из предыдующего параграфа следует, что:
| \( \small A'B'^2=(x_b-x_a)^2+(y_b-y_a)^2. \) | (11) |
Но AM=A'B'. Тогда из (10) и (11) следует:
| \( \small AB^2=AM^2+BM^2=A'B'^2+BM^2 \) \( \small =(x_b-x_a)^2+(y_b-y_a)^2+(z_b-z_a)^2. \) |
Откуда:
| \( \small AB= \sqrt{(x_b-x_a)^2+(y_b-y_a)^2+(z_b-z_a)^2}. \) | (12) |
Пример 3. В пространстве задана декартова прямоугольная система координат XOY и точки \( \small A(x_a; \ y_a ;\ z_a)=A(5;1;0) \) и \( \small B(x_b, \ y_b, \ z_b)=B(-8,-4;21). \) Найти рассояние между этими точками.
Решение. Для нахождения расстояния между точками A и B воспользуемся формулой (12). Подставляя координаты точек A и B в формулу (12), получим:
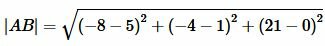 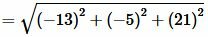 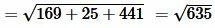 , , |
 . . |
Ответ:  .
.