Любая матрица A порядка m×n можно рассматривать как совокупность m векторов строк или n векторов столбцов.
Рангом матрицы A порядка m×n называется максимальное количество линейно независимых векторов столбцов или векторов строк.
Если ранг матрицы A равен r, то пишется:
rank(A)=r.
Пусть A произвольная матрица порядка m×n. Для нахождения ранга матрицы A применим к ней метод исключения Гаусса.
Отметим, что если на каком-то этапе исключения ведущий элемент окажется равным нулю, то меняем местами данную строку со строкой, в котором ведущий элемент отличен от нуля. Если окажется, что нет такой строки, то переходим к следующему столбцу и т.д.
После прямого хода исключения Гаусса получим матрицу, элементы которой под главной диагональю равны нулю. Кроме этого могут оказаться нулевые векторы строки.
Количество ненулевых векторов строк и будет рангом матрицы A.
Рассмотрим все это на простых примерах.
Найдем ранг следующей матрицы:

Умножив первую строку на 4 и прибавив ко второй строке и умножив первую строку на 2 и прибавив к третьей строке имеем:
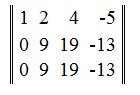
Вторую строку умножим на -1 и прибавим к третьей строке:

Получили две ненулевые строки и, следовательно ранг матрицы равен 2.
Найдем ранг следующей матрицы:

Умножим первую строку на -2 и прибавим ко второй строке. Аналогично обнулим элементы третьей и четвертой строки первого столбца:

Обнулим элементы третьей и четвертой строк второго столбца прибавляя соответствующие строки ко второй строке умноженной на число -1:

Наконец обнулим четвертый элемент четвертого столбца:
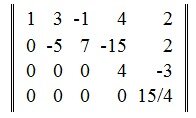
Получили четыре ненулевые строки. Следовательно ранг матрицы равен 4.
Для нахождения ранга матрицы пользуйтесь матричным онлайн калькулятором . Для подробного решения используйте калькулятор для вычиления ранга матрицы.