Скелетное разложение матрицы

Скелетное разложение матрицы A порядка m×n и ранга r - это представление матрицы A в виде произведения двух матриц B и C, где B - m×r -матрица C- r×n - матрица и rank(B)=r, rank(C)=r.

Пусть A m×n матрица произвольного ранга r. Тогда матрица A можно представить в виде произведения двух матриц:

A=BC,

(1)

где B m×r матрица ранга r и C - r×n матрица ранга r.

Для скелетного разложения матрицы A, в качестве строк матрицы С достаточно взять r линейно независимых строк матрицы A. Тогда каждая строка матрицы B можно найти из следующих систем линейных уравнений:

A₁=B₁C,

A₂=B₂C,

...

A_n=B_nC,

где A_i - i-ая строка матрицы A, B_i - i-ая строка матрицы B.

Так как C матрица полного ранга и составлен из векторов строк матрицы A, то матрицу B можно вичислить из следующего уравнения:

B=AC+,

(2)

где С⁺ псевдообратная к матрице C вычисляется из выражения

C⁺=C ^T(CC ^T)^-1.

Рассмотрим процесс скелетного разложения на численном примере.

Пример скелетного разложения матрицы

Приведем скелетное разложение матрицы

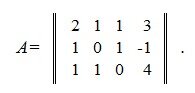
Для определения линейно независимых строк матрицы A, применим метод исключения Гаусса. Тогда матрица A примет следующий вид:

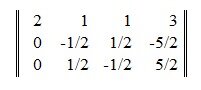
После второго шага исключения Гаусса, имеем:

Следовательно третья строка линейно зависима. Матрица C строится из всех линейно независимых векторов строк матрицы A:

Вычисляем псевдообратную к C матрицу C⁺:

Наконец, матрица B вычисляется из выражения (2):

Скелетное разложение матрицы онлайн

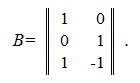
Для скелетного разложения матрицы пользуйтесь матричным онлайн калькулятором. Для этого постройте матрицу нужного порядка и введите данные. Далее нажмите на кнопку "скелетное разложение". В матрицах P и Q вы получите результат. Отметим, что для матриц A,P и Q справедливо равенство A=PQ.