LU-разложение матрицы A - это представление матрицы A в виде произведения
A=LU,
где L-нижняя треугольная матрица, U - верхняя треугольная или ступенчатая матрица.
Пусть A прямоугольная матрица порядка m×n любого ранга. С правой стороны матрицы А приписываем единичную матрицу E порядка m×m. Применяем к матрице A|E метод исключения Гаусса. Если на каком то этапе Гауссово исключения ведущий элемент равен нулю, и существует ненулевой элемент, расположенный ниже ведущего элемента, то LU - разложение данной матрицы невозможно. Если же элементы ниже ведущего элемента нулевые, то выбираем новый ведущий элемент той же строки и следующего столбца.
Приводим матрицу A|E к треугольному или ступенчатому виду. Получим матрицу U|L0, где U- верхняя треугольная или ступенчатая матрица, а L0- нижняя треугольная матрица. Заметим, что полученная матрица L0 приводит A к треугольному или ступенчатому виду:
|
L0A=U.
|
(1) |
Так как L0 квадратная невырожденная матрица, следовательно имеет обратную матрицу 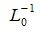 . Тогда
. Тогда
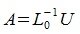 |
(2) |
или
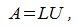 |
(3) |
где 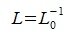 .
.
Как мы отметили, не всегда можно проводить LU -разложение матрицы. Но LUP- разложение всегда возможно.
LUP-разложение матрицы A - это представление матрицы A в виде произведения
PA=LU,
где L-нижняя треугольная матрица, U - верхняя треугольная или ступенчатая матрица, P- матрица перестановок (матрица перестановок - эта матрица, полученная из единичной матрицы перестановкой некоторых строк или столбцов).
Пусть A прямоугольная матрица порядка m×n любого ранга. С правой стороны матрицы А приписываем единичную матрицу E порядка m×m. Применяем к матрице A|E матод исключения Гаусса c выбором наибольшего по модулю ведущего элемента. Если на каком то этапе исключения ведущий элемент равен нулю, то процедуру останавливаем. Получим матрицу U|L0. Тогда имеют место равенства (1) и (2). Но в общем случае L0 и, следовательно, 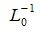 не являются нижними треугольными матрицами, если при применении Гауссово исключения строки переставлялись.
не являются нижними треугольными матрицами, если при применении Гауссово исключения строки переставлялись.
Далее допустим, что мы знаем, как построить матрицу A1 из матрицы A переставляя строки так, что при применении Гауссово исключения c выбором максимального по модулю ведущего элемента относительно матрицы A1 не понадобилась переставление строк. Выбираем матрицу перестановок так, что
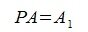 |
(4) |
Строим матрицу A1|E и применяем Гауссово исключение. Получим матрицу U|L1. Тогда
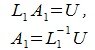 |
(5) |
где L1 и 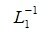 нижние треугольные матрицы т.к. при применении Гауссово исключения строки матрицы A1 не переставлялись.
нижние треугольные матрицы т.к. при применении Гауссово исключения строки матрицы A1 не переставлялись.
Из (4) и (5) имеем:
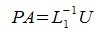 |
(6) |
Обозначим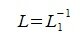 .
.
Наша задача найти L и U, без построения A1.
Из (2) и (4) имеем:
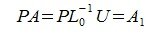 |
(7) |
Тогда, учитывая второе равенство (5), получим:
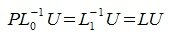 |
(8) |
Следовательно
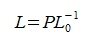 |
(9) |
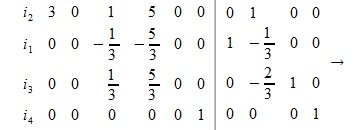
Получили, что для LUP-разложения нужно применить Гауссово исключение c выбором максимального по модулю ведущего элемента относительно матрицы A|E. Получим матрицу 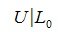 . Вычисляем обратную матрицу
. Вычисляем обратную матрицу 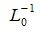 . Вычисляем L из выражения (9).
. Вычисляем L из выражения (9).
Матрица перестановок Р строится во время Гауссово исключения, учитывая перестановки строк.
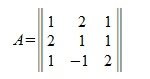

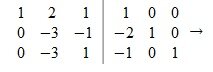
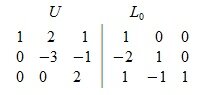
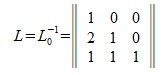








Для LU(LUP)-разложения онлайн пользуйтесь матричным онлайн калькулятором.