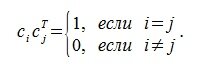Ортогональная матрица. Ортогонализация Грамма-Шмидта.

Квадратная матрица   i=1,2,...n,   j=1,2,...n называется ортогональной, если выполняется условие

AA^T=E,

где E - единичная матрица, A^T- транспонированная матрица.

Из условия AA^T=E следует, что A^T является обратной к матрице A:

A^-1=A^T.

Для любой невырожденной квадратной матрицы можно построить ортогональную матрицу. Для построения ортогональной матрицы применяют метод ортогонализации Грамма-Шмидта. Затем нормируют полученные векторы строки. Эти две процедуры вместе называют методом ортонормализации Грамма-Шмидта.

Ортогонализация Грамма-Шмидта

Пусть задана некоторая квадратная матрица, строки которой являются векторы

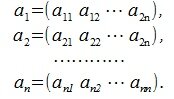
и пусть эти векторы линейно независимы (т.е. матрица построенная этими векторами строками невырождена). Требуется получить взаимно ортогональные n векторы

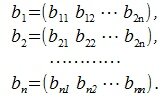
Суть метода заключается в следующем:

1. Выбирается некоторая строка (пусть это будет a₁). b₁ выбирается равным a₁.

2. Вектор b₂ получается пректированием a₂ на нуль-пространство b₁.

3. Вектор b₃ получается проектированием a₃ на нуль-пространство матрицы

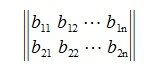
И т.д.

Рассмотрим подробнее процесс ортогонализации.

На первом шаге выбираем b₁=a₁.

На втором шаге вычисляем нуль-пространство b₁:

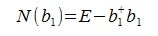
где E- единичная матрица порядка nxn,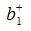-псевдообратная к b₁. Так как b₁ является вектором-строкой (матрицей-строкой), то

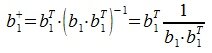
Для пректирования a₂ на нуль-пространство b₁ вычисляем

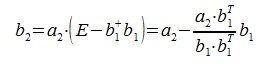
На третьем шаге вычисляем b₃:

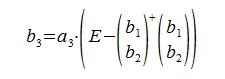
Так как векторы b₁ и b₂ ортогональны, то

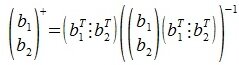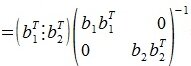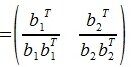Следовательно

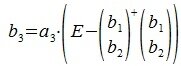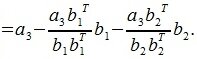Для n -го вектора получим:

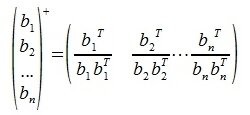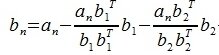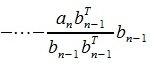Таким образом, процедура ортогонализации Грамма-Шмидта имеет следующий вид:

Ортонормализация Грамма-Шмидта

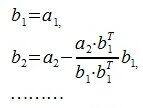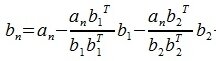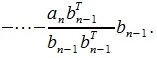Суть метода ортонормализации Грамма-Шмидта заключается в ортогонализации методом Грамма-Шмидта а затем нормализации полученных векторов строк:

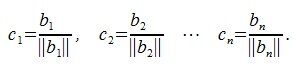
Полученная матрица

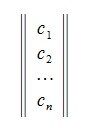
является ортогональной матрицей т.к.