Векторы x, y, ..., z называются линейно зависимыми векторами, если существуют числа α, β, ..., γ, из которых хотя бы одно отлично от нуля, такие что справедливо равенство:
|
αx+βy+...+γz=0.
|
(0) |
Другими словами линейная зависимость группы векторов означает, что существует среди них вектор, который можно представить линейной комбинацией других векторов этой группы.
Допустим 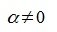 . Тогда
. Тогда
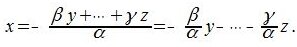
Следовательно вектор x линейно зависим из векторов этой группы.
Векторы x, y, ..., z называются линейно независимыми векторами, если из равенства (0) следует, что
α=β= ...= γ=0.
То есть группы векторов линейно независимы, если ни один вектор не может быть представлен линейной комбинацией других векторов этой группы.
Пусть заданы m векторов строк порядка n:
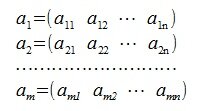 |
(1) |
Составим матрицу из этих векторов и добавим с правой стороны столбец, в котором запишем индексы соответствующих строк:
 |
(2) |
Сделав Гауссово исключение, приведем матрицу (2) к верхнему треугольному виду. Элементы последнего столбца изменяются только тогда, когда строки переставляются. После m шагов исключения получим:
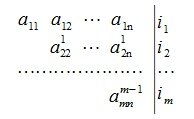
где i1, i2, ..., im - индексы строк, полученные при возможной перестановки строк. Рассматривая полученные строки из индексов строк исключаем те, которые соответствуют нулевым вектором строк. Оставшиеся строки образуют линейно независимые векторы. Отметим, что при составлении матрицы (2) изменяя последовательность векторов строк, можно получить другую группу линейно независимых векторов. Но подпространство, которую оба эти группы векторов образуют совпадают.
Для определения линейной зависимости векторов используйте матричный онлайн калькулятор .