Псевдообратная матрица

Для любой матрицы A, A⁺ является псевдообратной матрицей тогда и только тогда, когда выполнены следующие условия:

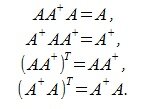(0)

Построение псевдообратной матрицы.

Пусть C r×n матрица, r<n и rank(C)=r. Тогда

C⁺=C^T(CC^T)^-1.

Пусть B m×r матрица, m>r и rank(B)=r. Тогда

B⁺=(B^TB)^-1B^T.

Для произвольной матрицы A порядка m×n и ранга r, псевдообратная матрица A⁺ можно получить следующим образом:

1. Производиться скелетное разложение матрицы A:

A=BC,

где B m×r матрица, rank(B)=r, C rxn матрица, rank(C)=r.

2. Строятся матрицы С⁺ и B⁺:

C⁺=C^T(CC^T)^-1,

B⁺=(B^TB)^-1B^T.

3. Матрица A⁺ вычисляется из следующего выражения:

A⁺=(BC)⁺=C⁺B⁺.

Заметим, что если A n×n матрица и rank(A)=n, то

A⁺=A^-1.

Пример вычисления псевдообратной матрицы

Рассмотрим пример из раздела скелетное разложение матрицы:

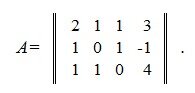
Для построения псевдообратной матрицы сделаем скелетное разложение:

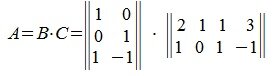
Тогда 

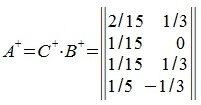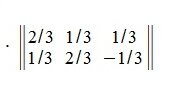Подставляя A и A⁺ в уравнения (0), можно убедиться, что A⁺ является псевдообратной к A матрицей.

Решение системы линейных уравнений с помощью псевдообратной матрицы

Пусть задана система линейных уравнений

Ax=b.

(1)

где A - m×n - матрица, x∈Rⁿ, b∈R^m.

Найдем решение системы (1), если оно существует.

Перепишем систему (1) в следующем виде:

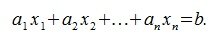(2)

где - векторы столбцы матрицы A, 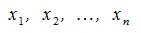- координаты вектора x.

Из системы (2) следует, что для того, чтобы система (1) имела решение вектор b должен быть линейной комбинацией векторов столбцов матрицы A c коэффициентами 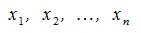. Таким образом, можно записать, что для совместности системы (1) должно выполняться условие

b∈R(A),

(3)

где R(A) - пространство столбцов матрицы A.

Построим псевдообратную к A матрицу A⁺. Рассмотрим вектор

x'=A+b.

(4)

Подставим (4) в систему (1):

AA+b=b.

(5)

Если система совместна, т.е. если выполнено условие (3), то R(AA⁺)≡R(A) и, следовательно, справедливо равенство (5) и x' является решением (1).

Онлайн нахождение псевдообратной матрицы

Для нахождения псевдообратной матрицы пользуйтесь матричным онлайн калькулятором .