Норма матрицы

Рассмотрим произвольную матрицу A порядка m×n и связанную с нею линейное преобразование y=Ax, где x∈Vⁿ, y∈U^m. Введем в этих пространствах нормы векторов , .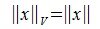

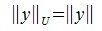Определим норму матрицы A равенством:

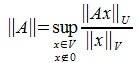(1)

Из определения нормы матрицы следует:

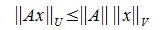(2)

Пусть для двух матриц A и B порядка m×n определены одни и те же векторные нормы. Тогда имеем соотношение:

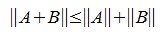(3)

Кроме того справедливо равенство

,

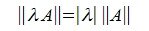(4)

где λ любое число.

Пусть для m×n матрицы A и n×k матрицы B определены матричные нормы 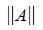, 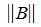и пусть для m×k матрицы AB определена норма 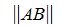. Тогда

.

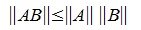Вычислим норму матрицы A , введя в пространствах V и U конкретные векторные нормы.

1. Пусть в пространствах V и U введена векторная норма

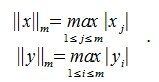
Тогда

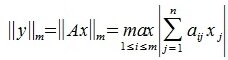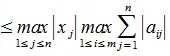(5)

или

,

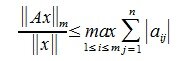(6)

В (5) и (6) неравнетство превращается в равенство, если взять 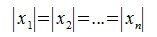и 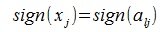, j=1,...,n, где l-то значение i, при котором

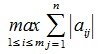
достигает своего максимума. Учитывая высшеизложенное, неравенство (6) и равенство (1), получим:

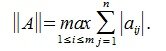(7)

2. Введем в пространствах V и U векторную норму

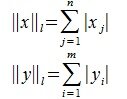
Тогда

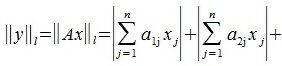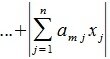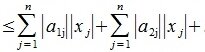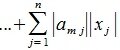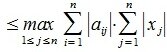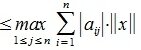или

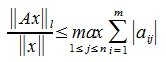(8)

Пусть 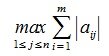достигается при j=l. Для вектора x, у которого только один элемент отлично от нуля, имеем:

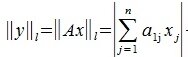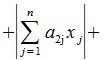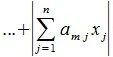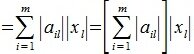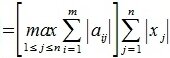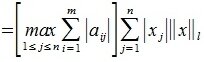(9)

Учитывая (1),(8) и (9) получим l-норму матрицы A:

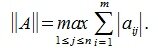(10)

Норму матрицы, определяемую с помощью формулы (1), называется операторной нормой, подчиненной данной норме векторов.

Отметим, что определение нормы матрицы (1) эквивалентно следующему определению:

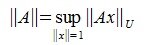(11)

Действительно, любой ненулевой вектор x∈V можно представить в виде произведения λx₁, где 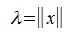, 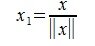. Тогда, учитывая, что 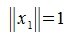, получим:

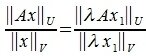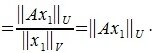(12)

Примеры вычисления нормы матрицы

Вычислим m-норму и l-норму матрицы используя (7) и (10).

Геометрическая интерпретация нормы матрицы

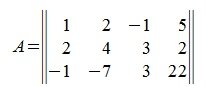
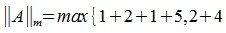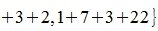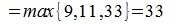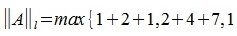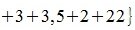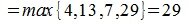Пусть в линейном пространстве V введена m-норма для всех векторов x∈V:

.

Найдем норму матрицы

.

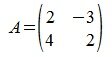Рассмотрим множество всех векторов, которые имеют норму 1. В двухмерном пространстве это те векторы конечные точки которых находятся на квадрате на рис. 1. Обозначим это множество символом X₀.

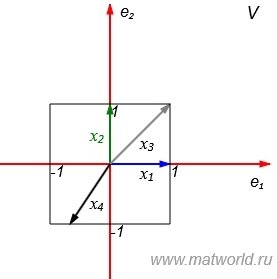
Рис. 1

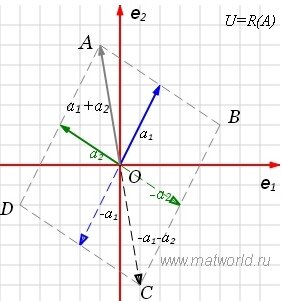
Рис. 2

 

На рисунке рис. 2 изображено пространство столбцов матрицы A. Каждому вектору x∈X₀ соответствует вектор Ax в U. Конечные точки этих векторов находятся на пунктирном четырехугольнике ABCD. m-норма матрицы A - это модуль наибольшго координата наибольшего из векторов, конечная точка которого находится на четырехугольнике ABCD. На рис.2 это векторы 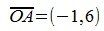и 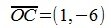а модуль наибольшего координата 6. Используя (3), аналитически получим тот же результат.

Отметим, что норма матрицы показывает насколько максимально растягивается вектор x при отображении y=Ax. В нашем примере векторы х растягиваются максимально 6 раз.