Норма (модуль, длина) вектора

В пространстве V каждому вектору x∈V ставим в соответствие некоторое неотрицательное число 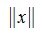так, чтобы для произвольных векторов x,y ∈V и произвольного скаляра λ выполнялись следующие условия:

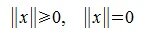1. тогда и только тогда, когда x=0.
2. .
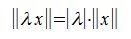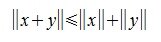3. (неравенство треугольника).

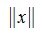называется нормой (длиной, модулем) вектора x∈V .

Примеры норм в линейных пространствах

1. max-норма, или m – норма:   

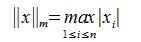
2. l-норма:    

3. Евклидова норма:    

Пример вычисления нормы (длины, модуля) вектора

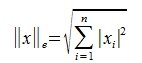
Вычислим нормы вектора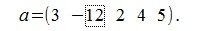

1. m-норма:

2. l-норма: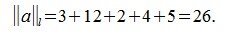

3. Евклидова норма: